SLAS669E September   2010  – may 2020 ADS5400-SP

PRODUCTION DATA.  

  1. 1 Features
  2. 2 Applications
  3. 3 Description
    1.     Block Diagram
  4. 4 Revision History
  5. 5 Pin Configuration and Functions
    1.     Pin Functions
  6. 6 Specifications
    1. 6.1 Absolute Maximum Ratings
    2. 6.2 ESD Ratings
    3. 6.3 Recommended Operating Conditions
    4. 6.4 Thermal Information
    5. 6.5 Electrical Characteristics
    6. 6.6 Switching Characteristics
    7. 6.7 Timing Characteristics
    8. 6.8 Interleaving Adjustments
    9. 6.9 Typical Characteristics
  7. 7 Detailed Description
    1. 7.1 Overview
    2. 7.2 Functional Block Diagram
    3. 7.3 Feature Description
      1. 7.3.1  Input Configuration
      2. 7.3.2  Voltage Reference
      3. 7.3.3  Analog Input Over-Range Recovery Error
      4. 7.3.4  Clock Inputs
      5. 7.3.5  Over Range
      6. 7.3.6  Data Scramble
      7. 7.3.7  Test Patterns
      8. 7.3.8  Die Identification and Revision
      9. 7.3.9  Die Temperature Sensor
      10. 7.3.10 Interleaving
        1. 7.3.10.1 Gain Adjustment
        2. 7.3.10.2 Offset Adjustment
        3. 7.3.10.3 Input Clock Coarse Phase Adjustment
        4. 7.3.10.4 Input Clock Fine Phase Adjustment
    4. 7.4 Device Functional Modes
      1. 7.4.1 Output Bus and Clock Options
      2. 7.4.2 Reset and Synchronization
      3. 7.4.3 LVDS
    5. 7.5 Programming
      1. 7.5.1 Serial Interface
        1. Table 2. Instruction Byte of the Serial Interface
    6. 7.6 Serial Register Map
      1. 7.6.1 Description of Serial Registers
  8. 8 Application and Implementation
    1. 8.1 Application Information
    2. 8.2 Typical Application
      1. 8.2.1 Design Requirements
      2. 8.2.2 Detailed Design Procedure
        1. 8.2.2.1 Clocking Source for ADS5400-SP
        2. 8.2.2.2 Amplifier Selection
      3. 8.2.3 Application Curve
  9. 9 Power Supply Recommendations
  10. 10Layout
    1. 10.1 Layout Guidelines
    2. 10.2 Layout Example
  11. 11Device and Documentation Support
    1. 11.1 Device Support
      1. 11.1.1 Device Nomenclature
        1. 11.1.1.1 Definition of Specifications
    2. 11.2 Documentation Support
    3. 11.3 Receiving Notification of Documentation Updates
    4. 11.4 Support Resources
    5. 11.5 Trademarks
    6. 11.6 Electrostatic Discharge Caution
    7. 11.7 Glossary
  12. 12Mechanical, Packaging, and Orderable Information

封装选项

机械数据 (封装 | 引脚)
散热焊盘机械数据 (封装 | 引脚)
订购信息

8.2.2.2 Amplifier Selection

The amplifier and any input filtering will have its own SNR performance, and the SNR performance of the amplifier front end will combine with the SNR of the ADC itself to yield a system SNR that is less than that of the ADC itself. System SNR can be calculated from the SNR of the amplifier conditioning circuit and the overall ADC SNR as in Equation 7. In Equation 7, the SNR of the ADC would be the value derived from the datasheet specifications and the clocking derivation presented in the previous section.

Equation 7. ADS5400-SP eq_04_slas611.gif

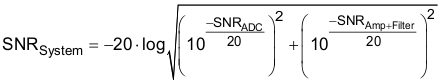
The signal-to-noise ratio (SNR) of the amplifier and filter can be calculated from the noise specifications in the datasheet for the amplifier, the amplitude of the signal and the bandwidth of the filter. The noise from the amplifier is band-limited by the filter and the rolloff of the filter will depend on the order of the filter, so it is convenient to replace the filter rolloff with an equivalent brick-wall filter bandwidth. For example, a 1st order filter may be approximated by a brick-wall filter with bandwidth of 1.57 times the bandwidth of the 1st order filter. Assume a 1st order filter for this design. The amplifier and filter noise can be calculated using Equation 8.

Equation 8. ADS5400-SP eq_05_slas611.gif

where

  • VO= the amplifier output signal (which will be full scale input of the ADC expressed in rms)
  • EFILTEROUT = ENAMPOUT × √ENB
    • ENAMPOUT = the output noise density of the LMH3401 (3.4 nV/√Hz)
    • ENB = the brick-wall equivalent noise bandwidth of the filter

In Equation 8, the parameters of the equation may be seen to be in terms of signal amplitude in the numerator and amplifier noise in the denominator, or SNR. For the numerator, use the full scale voltage specification of the ADS5400-SP, or 2 V peal to peak differential. Because Equation 8 requires the signal voltage to be in rms, convert 2 VPP to 0.706 V rms.

The noise specification for the LMH3401 is listed as 3.4 nV/√Hz, therefore, use this value to integrate the noise component from DC out to the filter cutoff, using the equivalent brick wall filter of 400 MHz × 1.57, or 628 MHz. 3.4 nV/√Hz integrated over 628 MHz yields 85204 nV, or 85.204 µV.

Using 0.706 V rms for VO and 85.204 µV for EFILTEROUT, (see Equation 8) the SNR of the amplifier and filter as given by Equation 8 is approximately 78.4 dB.

Taking the SNR of the ADC as 58.8 dB from Figure 40, and SNR of the amplifier and filter as 78.4 dB, Equation 7 predicts the system SNR to be 58.75 dB. In other words, the SNR of the ADC and the SNR of the front end combine as the square root of the sum of squares, and because the SNR of the amplifier front end is much greater than the SNR of the ADC in this example, the SNR of the ADC dominates Equation 7 and the system SNR is almost the same as the SNR of the ADC. The assumed design requirement is 58 dB, and after a clocking solution was selected and an amplifier or filter solution was selected, the predicted SNR is 58.75 dBFS.

千亿体育app官网登录(中国)官方网站IOS/安卓通用版/手机APP | 米乐app下载官网（中国）|ios|Android/通用版APP最新版 | 米乐|米乐·M6（中国大陆）官方网站 | 千亿体育登陆地址 | 华体会体育（中国）HTH·官方网站 | 千赢qy国际_全站最新版千赢qy国际V6.2.14安卓/IOS下载 | 18新利网v1.2.5|中国官方网站 | bob电竞真人（中国官网）安卓/ios苹果/电脑版【1.97.95版下载】 | 千亿体育app官方下载(中国)官方网站IOS/安卓/手机APP下载安装 |