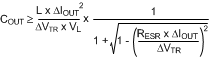8.1.3 Output Capacitor Selection (C_OUT)

The output capacitor, C_OUT, filters the inductor ripple current and provides a source of charge for transient load events. A wide range of output capacitors may be used with the LM27402 that provide excellent performance, including ceramic, tantalum, or electrolytic type chemistries. Typically, ceramic capacitors provide extremely low ESR to reduce the output ripple voltage and noise spikes, while tantalum and electrolytic capacitors provide a large bulk capacitance in a small size for transient loading events. When selecting the output capacitance, the two performance characteristics to consider are output voltage ripple and transient response. The output voltage ripple is approximated by Equation 3:

Equation 3.

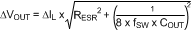
where ΔV_OUT is the amount of peak-to-peak voltage ripple at the power supply output, R_ESR is the equivalent series resistance of the output capacitor, f_SW is the switching frequency, and C_OUT is the output capacitance used in the design. The tolerable output ripple amplitude is application specific; however a general recommendation is to keep the output ripple less than 1% of the rated output voltage. Note that ceramic capacitors are sometimes preferred because they have very low ESR; however, depending on package and voltage rating of the capacitor, the effective in-circuit capacitance can drop significantly with applied voltage and operating temperature.

The output capacitor also affects the output voltage deviation during a load current transient. The peak output voltage deviation is dependent on many factors such as output capacitance, output capacitor ESR, filter inductance, control loop bandwidth, powertrain parasitics, and so on. Given sufficient control loop bandwidth, a good approximation of the output voltage deviation is seen in Equation 4:

Equation 4.

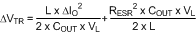
ΔV_TR is the transient output voltage deviation, ΔI_OUT is the load current step change and L is the filter inductance. V_L is the minimum inductor voltage, which is duty ratio dependent.

V_L = V_OUT , if D ≤ 0.5,

V_L = V_IN - V_OUT , if D > 0.5

For a desired ΔV_TR, a minimum output capacitance is found by Equation 5:

Equation 5.