8.3.8 Control Loop Compensation

The control loop is modeled as most typical current mode controllers. Using a first order approximation, the uncompensated loop can be modeled as a single pole created by the output capacitor and, in the boost and buck-boost topologies, a right half plane zero created by the inductor, where both have a dependence on the LED string dynamic resistance. There is also a high-frequency pole in the model; however, it is near the switching frequency and plays no part in the compensation design process. Therefore, it is neglected. Because ceramic capacitance is recommended for use with LED drivers, due to long lifetimes and high ripple current rating, the ESR of the output capacitor can also be neglected in the loop analysis. The DC gain of the uncompensated loop depends on internal controller gains and the external sensing network.

This section describes a buck-boost regulator as an example case.

Use Equation 12 to calculate the uncompensated loop gain for a buck-boost regulator.

Equation 12.

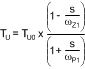
Where the uncompensated DC loop gain of the system is calculated using Equation 13.

Equation 13.

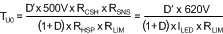
And the output pole (ω_P1) is approximated using Equation 14.

Equation 14.

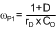
And the right half plane zero (ω_Z1) is:

Equation 15.

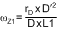
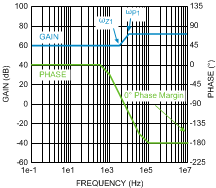Figure 17. Uncompensated Loop Gain Frequency Response

Figure 17 shows the uncompensated loop gain in a worst-case scenario when the RHP zero is below the output pole. This occurs at high duty cycles when the regulator is trying to boost the output voltage significantly. The RHP zero adds 20dB/decade of gain while losing 45°/decade of phase, which places the crossover frequency (when the gain is zero dB) extremely high because the gain only starts falling again due to the high-frequency pole (not shown in Figure 17). The phase is below –180° at the crossover frequency, which means there is no phase margin (180° + phase at crossover frequency) causing system instability. Even if the output pole is below the RHP zero, the phase reaches –180° before the crossover frequency in most cases yielding instability.

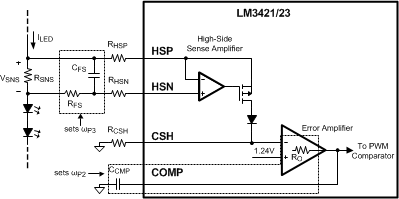Figure 18. Compensation Circuitry

To mitigate this problem, a compensator should be designed to give adequate phase margin (above 45°) at the crossover frequency. A simple compensator using a single capacitor at the COMP pin (C_CMP) adds a dominant pole to the system, which ensures adequate phase margin if placed low enough. At high duty cycles (as shown in Figure 17), the RHP zero places extreme limits on the achievable bandwidth with this type of compensation. However, because an LED driver is essentially free of output transients (except catastrophic failures open or short), the dominant pole approach, even with reduced bandwidth, is usually the best approach. The dominant compensation pole (ω_P2) is determined by C_CMP and the output resistance (R_O) of the error amplifier (typically 5 MΩ) as demonstrated in Equation 16.

Equation 16.

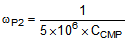
It may also be necessary to add one final pole at least one decade above the crossover frequency to attenuate switching noise and, in some cases, provide better gain margin. This pole can be placed across R_SNS to filter the ESL of the sense resistor at the same time. Figure 18 shows how the compensation is physically implemented in the system.

The high-frequency pole (ω_P3) can be calculated using Equation 17.

Equation 17.

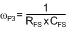
The total system transfer function becomes:

Equation 18.

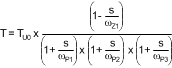
The resulting compensated loop gain frequency response shown in Figure 19 indicates that the system has adequate phase margin (above 45°) if the dominant compensation pole is placed low enough, ensuring stability.

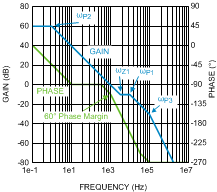Figure 19. Compensated Loop Gain Frequency Response