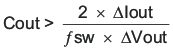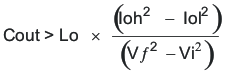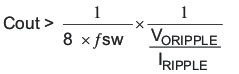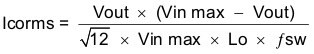8.2.1.2.4 Output Capacitor

There are three primary considerations for selecting the value of the output capacitor. The output capacitor will determine the modulator pole, the output voltage ripple, and how the regulators responds to a large change in load current. The output capacitance needs to be selected based on the more stringent of these three criteria.

The desired response to a large change in the load current is the first criteria. The output capacitor needs to supply the load with current when the regulator can not. This situation would occur if there are desired hold-up times for the regulator where the output capacitor must hold the output voltage above a certain level for a specified amount of time after the input power is removed. The regulator also will temporarily not be able to supply sufficient output current if there is a large, fast increase in the current needs of the load such as transitioning from no load to a full load. The regulator usually needs two or more clock cycles for the control loop to see the change in load current and output voltage and adjust the duty cycle to react to the change. The output capacitor must be sized to supply the extra current to the load until the control loop responds to the load change. The output capacitance must be large enough to supply the difference in current for 2 clock cycles while only allowing a tolerable amount of droop in the output voltage. Equation 32 shows the minimum output capacitance necessary to accomplish this.

Where ΔIout is the change in output current, ƒsw is the regulators switching frequency and ΔVout is the allowable change in the output voltage. For this example, the transient load response is specified as a 3% change in Vout for a load step from 1.5 A to 2.5 A (full load). For this example, ΔIout = 2.5-1.5 = 1.0 A and
ΔVout = 0.03 × 3.3 = 0.099 V. Using these numbers gives a minimum capacitance of 67 μF. This value does not take the ESR of the output capacitor into account in the output voltage change. For ceramic capacitors, the ESR is usually small enough to ignore in this calculation. Aluminum electrolytic and tantalum capacitors have higher ESR that should be taken into account.

The catch diode of the regulator can not sink current so any stored energy in the inductor will produce an output voltage overshoot when the load current rapidly decreases, see Figure 51. The output capacitor must also be sized to absorb energy stored in the inductor when transitioning from a high load current to a lower load current. The excess energy that gets stored in the output capacitor will increase the voltage on the capacitor. The capacitor must be sized to maintain the desired output voltage during these transient periods. Equation 33 is used to calculate the minimum capacitance to keep the output voltage overshoot to a desired value. Where L is the value of the inductor, I_OH is the output current under heavy load, I_OL is the output under light load, Vf is the final peak output voltage, and Vi is the initial capacitor voltage. For this example, the worst case load step will be from 2.5 A to 1.5 A. The output voltage will increase during this load transition and the stated maximum in our specification is 3 % of the output voltage. This will make Vf = 1.03 × 3.3 = 3.399. Vi is the initial capacitor voltage which is the nominal output voltage of 3.3 V. Using these numbers in Equation 33 yields a minimum capacitance of 60 μF.

Equation 34 calculates the minimum output capacitance needed to meet the output voltage ripple specification. Where fsw is the switching frequency, V_oripple is the maximum allowable output voltage ripple, and I_ripple is the inductor ripple current. Equation 34 yields 12 μF.

Equation 35 calculates the maximum ESR an output capacitor can have to meet the output voltage ripple specification. Equation 35 indicates the ESR should be less than 36 mΩ.

The most stringent criteria for the output capacitor is 67 μF of capacitance to keep the output voltage in regulation during an load transient.

Additional capacitance de-ratings for aging, temperature and dc bias should be factored in which will increase this minimum value. For this example, 2 x 47 μF, 10 V ceramic capacitors with 3 mΩ of ESR will be used. The derated capacitance is 72.4 µF, above the minimum required capacitance of 67 µF.

Capacitors generally have limits to the amount of ripple current they can handle without failing or producing excess heat. An output capacitor that can support the inductor ripple current must be specified. Some capacitor data sheets specify the Root Mean Square (RMS) value of the maximum ripple current. Equation 36 can be used to calculate the RMS ripple current the output capacitor needs to support. For this application, Equation 36 yields 238 mA.

Equation 32.

Equation 33.

Equation 34.

Equation 35.

Equation 36.