ZHCSF61B October 2015 – June 2017 TPS65321-Q1
PRODUCTION DATA.
- 1 特性
- 2 应用
- 3 说明
- 4 修订历史记录
- 5 Pin Configuration and Functions
- 6 Specifications
-
7 Detailed Description
- 7.1 Overview
- 7.2 Functional Block Diagram
- 7.3
Feature Description
- 7.3.1
Buck Regulator
- 7.3.1.1 Fixed-Frequency PWM Control
- 7.3.1.2 Slope Compensation Output
- 7.3.1.3 Pulse-Skip Eco-mode™ Control Scheme
- 7.3.1.4 Dropout Mode Operation and Bootstrap Voltage (BOOT)
- 7.3.1.5 Error Amplifier
- 7.3.1.6 Voltage Reference
- 7.3.1.7 Adjusting the Output Voltage
- 7.3.1.8 Soft-Start Pin (SS)
- 7.3.1.9 Reset Output, nRST
- 7.3.1.10 Overload-Recovery Circuit
- 7.3.1.11 Constant Switching Frequency and Timing Resistor (RT/CLK Pin)
- 7.3.1.12 Overcurrent Protection and Frequency Shift
- 7.3.1.13 Selecting the Switching Frequency
- 7.3.1.14 How to Interface to RT/CLK Pin
- 7.3.1.15 Overvoltage Transient Protection
- 7.3.1.16 Small-Signal Model for Loop Response
- 7.3.1.17 Simple Small-Signal Model for Peak-Current Mode Control
- 7.3.1.18 Small-Signal Model for Frequency Compensation
- 7.3.2 LDO Regulator
- 7.3.3 Thermal Shutdown
- 7.3.4 Enable and Undervoltage Lockout
- 7.3.1
Buck Regulator
- 7.4 Device Functional Modes
-
8 Application and Implementation
- 8.1 Application Information
- 8.2
Typical Application
- 8.2.1
2.2-MHzSwitching Frequency, 9-V to 16-V Input, 3.3-V Output Buck Regulator, 5-V Output LDO Regulator
- 8.2.1.1 Design Requirements
- 8.2.1.2
Detailed Design Procedure
- 8.2.1.2.1 Switching Frequency Selection for the Buck Regulator
- 8.2.1.2.2 Output Inductor Selection for the Buck Regulator
- 8.2.1.2.3 Output Capacitor Selection for the Buck Regulator
- 8.2.1.2.4 Catch Diode Selection for the Buck Regulator
- 8.2.1.2.5 Input Capacitor Selection for the Buck Regulator
- 8.2.1.2.6 Soft-Start Capacitor Selection for the Buck Regulator
- 8.2.1.2.7 Bootstrap Capacitor Selection for the Buck Regulator
- 8.2.1.2.8 Output Voltage and Feedback Resistor Selection for the Buck Regulator
- 8.2.1.2.9 Frequency Compensation Selection for the Buck Regulator
- 8.2.1.2.10 LDO Regulator
- 8.2.1.2.11 Power Dissipation
- 8.2.1.2.12 Power Dissipation Losses of the LDO Regulator
- 8.2.1.2.13 Total Device Power Dissipation Losses and Junction Temperature
- 8.2.1.3 Application Curves
- 8.2.2 Design Example With 500-kHz Switching Frequency
- 8.2.1
2.2-MHzSwitching Frequency, 9-V to 16-V Input, 3.3-V Output Buck Regulator, 5-V Output LDO Regulator
- 9 Power Supply Recommendations
- 10Layout
- 11器件和文档支持
- 12机械、封装和可订购信息
封装选项
请参考 PDF 数据表获取器件具体的封装图。
机械数据 (封装 | 引脚)
- PWP|14
散热焊盘机械数据 (封装 | 引脚)
- PWP|14
订购信息
8 Application and Implementation
NOTE
Information in the following applications sections is not part of the TI component specification, and TI does not warrant its accuracy or completeness. TI’s customers are responsible for determining suitability of components for their purposes. Customers should validate and test their design implementation to confirm system functionality.
8.1 Application Information
The TPS65321-Q1 buck regulator operates with a supply voltage of 3.6 V to 36 V. The TPS65321-Q1 LDO regulator operates with a supply voltage of 3 V to 36 V V. To reduce power dissipation, TI recommends to use the output voltage of the buck regulator as the input supply for the LDO regulator. To use the output voltage of the buck regulator in this way, the selected buck-regulator output voltage must be higher than the selected LDO-regulator output voltage.
To optimize the switching performance (such as low jitter) in automotive applications with input voltages that have wide ranges, TI recommends to operate the device at higher frequencies, such as 2 MHz, which also helps achieve AM-band compliance requirements (that extends until 1.7 MHz).
8.1.1 Soft-Start Discharge
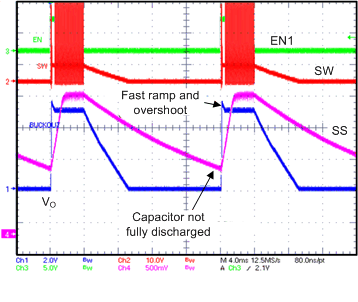
A potential set of conditions for the TPS65321-Q1 device can cause the soft-start capacitor to not (fully) discharge. A runtime condition can shorten the effective discharge time so that the external capacitor is not adequately discharged.
To determine if a system is impacted by the inadequate soft-start (SS) discharge, evaluate the system to assess whether or not an event occurred. If no event occurred, systems that always remain on are not affected. This issue is only triggered by an EN1 pin toggle. Systems where the TPS65321-Q1 device is completely powered off are not affected. Systems with several minutes or hours (depending on the selected SS capacitor, see the Soft-Start Capacitor Selection for the Buck Regulator section) of delay between when the EN1 pin toggles are not affected.
No corrective action is required if the downstream hardware can handle all of the following:
- VIN-overshoot (up to 1 V was observed, see Figure 15)
- A nonmonotonous ramp (see Figure 16)
- High inrush-current (up to 6 A, see Figure 16)
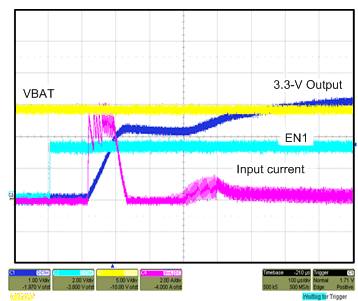
If the system is affected, the following solutions are available:
- Implement an application fix by applying a discharge resistor (at least 2 MΩ) in parallel to the SS capacitor on the SS pin. For additional information, see the Passive Discharge Through a Resistor in Parallel With the SS Capacitor section.
- Implement an application fix by applying an external discharge circuit (such as one with two NPN transistors). For additional information, see the Active Discharge Through A NPN Transistor section.
NOTE
This resistance discharges the capacitor, but requires a finite time to do so.
No corrective action is required if the off time is long enough to allow the leakage current to discharge SS-capacitor, or if the downstream hardware can accept nonmonotonous ramp, overshoot on VO, increased inrush-currents, or all of these.
8.1.2 Passive Discharge Through a Resistor in Parallel With the SS Capacitor
Implement an application fix by applying a discharge resistor (at least 2-MΩ) in parallel to the SS capacitor on the SS pin as shown in Figure 17.
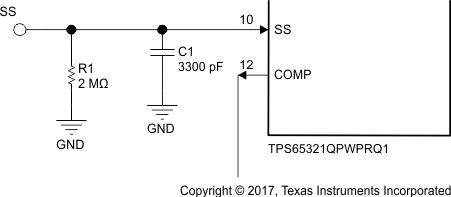 Figure 17. Passive Discharge Schematic
Figure 17. Passive Discharge Schematic
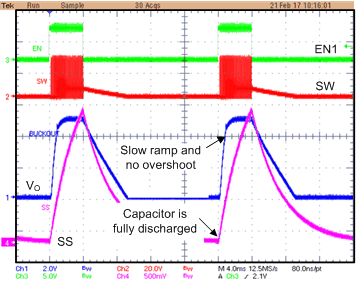 Figure 18. Passive Discharge With 2-MΩ Resistor
Figure 18. Passive Discharge With 2-MΩ Resistor
The benefits of this option include a simple, rugged solution. However, the disadvantages include the following:
- If maximum resistor values apply (in automotive applications, the maximum is often 100 kΩ), multiple resistors in series are required to achieve the 2-MΩ minimum value.
- This resistance discharges the capacitor, but requires a finite time to do so. For example, a capacitor discharge time of 3.3 nF with a 2-MΩ resistor is approximately 30 ms. A capacitor discharge time of 10-nF with a 2-MΩ resistor is approximately 80 ms. Use Equation 22 to calculate the discharge time of the selected capacitor. Online tools are available to help with the calculation.
- R is the discharge resistor (2 MΩ).
- C is the value of the soft-start capacitor (for example, 3.3 nF or 10 nF).
- A permanent current will flow from the SS-current source through the resistor, increasing the quiescent current.
where
When implementing this solution, calculate the discharge time of the capacitor, and do not re-enable the buck-converter before this time has elapsed. When taking measurements, consider the impedance of the instrument. For example, a passive Oscilloscope-probehead usually has a 1-MΩ impedance and compromises measurement accuracy as it significantly contributes to the discharge if probing the SS pin.
8.1.3 Active Discharge Through A NPN Transistor
Implement an active discharge, activated by the EN1 signal as shown in Figure 19. In this solution, the Q1 transistor functions as an inverter and must be supplied by an always-on source, which is VBAT in this case. The Q2 transistor discharges the SS capacitor.
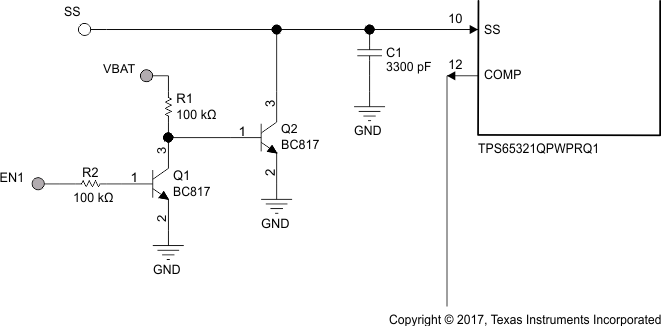 Figure 19. Active Discharge Schematic
Figure 19. Active Discharge Schematic
The benefits of this option include fast discharge. However, the disadvantages include the following:
- More external components
- Increased quiescent current through the Q1 transistor which can be mitigated by the selected value for R1.
When implementing this solution, the selected transistor must have a leakage current of less than 1 µA when turned off, and have a high enough forward-voltage drop on Q1 and a low enough turnon voltage on the Q2 transistor to turn on Q2 (therefore bipolar transistors are used instead of MOSFETs). The combination of resistors, transistors, VBAT-range, and EN1-drive-voltage must be validated (for example, a low value for R1 with a high value for R2 and a low EN1 voltage might not (fully) turn on Q2 and therefore not discharge the SS capacitor). The a value of 100 kΩ for both resistors proved valid across a wide range of permutations with the selected BC817-transistors. When taking measurements, consider the impedance of the instrument. For example, a passive Oscilloscope-probehead usually has a 1-MΩ impedance and compromises measurement accuracy as it significantly contributes to the discharge if probing the SS pin.
8.2 Typical Application
8.2.1 2.2-MHzSwitching Frequency, 9-V to 16-V Input, 3.3-V Output Buck Regulator, 5-V Output LDO Regulator
This example details the design of a high-frequency switching regulator and linear regulator using ceramic output capacitors.
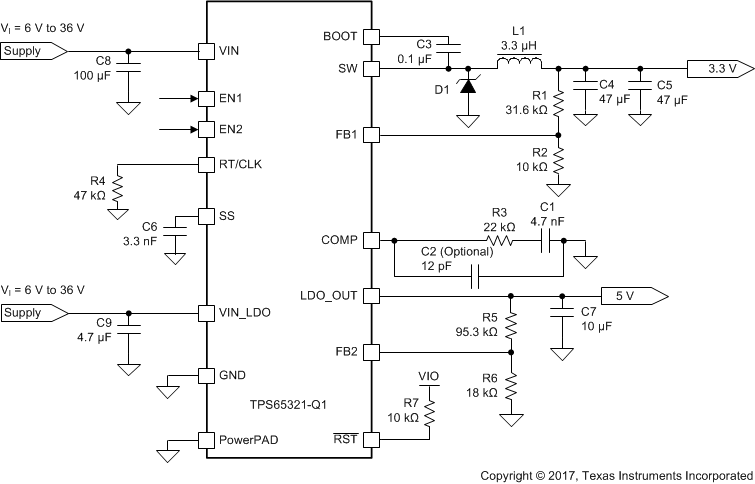 Figure 20. TPS65321-Q1 Design Example With 2.2-MHz Switching Frequency
Figure 20. TPS65321-Q1 Design Example With 2.2-MHz Switching Frequency
8.2.1.1 Design Requirements
A few parameters must be known to begin the design process. The determination of these parameters is typically at the system level. This example begins with the parameters listed in Table 3.
Table 3. Design Requirements
| DESIGN PARAMETER | EXAMPLE VALUE |
|---|---|
| Input voltage, VIN1 | 6 V to 36 V, nominal 12 V |
| Output voltage, VREG1 (buck regulator) | 3.3 V ± 2% |
| Maximum output current, IO_max1 | 3 A |
| Minimum output current, IO_min1 | 0.01 A |
| Transient response, 0.01 A to 0.8 A | 3% |
| Output ripple voltage | 1% |
| Switching frequency, ƒSW | 2.2 MHz |
| Input voltage, VIN_LDO | 6 V to 36 V, nominal 12 V |
| Output voltage, VREG2 (LDO regulator) | 5 V ± 2% |
8.2.1.2 Detailed Design Procedure
8.2.1.2.1 Switching Frequency Selection for the Buck Regulator
The first step is to decide on a switching frequency for the regulator. Typically, the user selects the highest switching frequency possible because this produces the smallest solution size. The high switching frequency allows for lower-valued inductors and smaller output capacitors compared to a power supply that switches at a lower frequency. The selectable switching frequency is limited by the minimum on-time of the internal power switch, the input voltage, the output voltage, and the frequency-shift limitation.
Consider minimum on-time and frequency-shift protection as calculated with Equation 4 and Equation 5. To find the maximum switching frequency for the regulator, select the lower value of the two results. Switching frequencies higher than these values result in pulse skipping or the lack of overcurrent protection during a short circuit. The typical minimum on-time, tON-min, is 100 ns for the TPS65321-Q1 device. For this example, where the output voltage is 3.3 V and the maximum input voltage is 36 V, use a switching frequency of 2200 kHz. Use Equation 3 to calculate the timing resistance for a given switching frequency. The R4 resistor sets the switching frequency. A 2.2-MHz switching frequency requires a 47-kΩ resistor (see R4 in Figure 20).
8.2.1.2.2 Output Inductor Selection for the Buck Regulator
Use Equation 23 to calculate the minimum value of the output inductor. The output capacitor filters the inductor ripple current. Therefore, selecting high inductor-ripple currents impacts the selection of the output capacitor because the output capacitor must have a ripple-current rating equal to or greater than the inductor ripple current. In general, the inductor ripple value is at the discretion of the designer; however, the following guidelines can be used to select this value. KIND is a coefficient that represents the amount of inductor ripple current relative to the maximum output current.
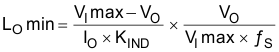
For designs using low-ESR output capacitors such as ceramics, use a value as high as KIND = 0.3. When using higher-ESR output capacitors, KIND = 0.2 yields better results. In a wide-input voltage regulator, selecting an inductor ripple current on the larger side is best because it allows the inductor to still have a measurable ripple current with the input voltage at a minimum.
For this design example, use KIND = 0.2 and the minimum inductor value which is calculated as 2.27 µH. For this design, select standard value which is 3.3 µH (see L1 in Figure 20). Use Equation 24 to calculate the inductor ripple current (Iripple). For the output filter inductor, do not to exceed the RMS-current and saturation-current ratings. Use Equation 25 and Equation 26 to calculate the RMS current (IL-RMS) and the peak inductor (IL-peak).
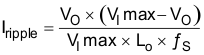
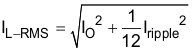
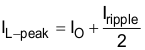
For this design, the RMS inductor current is 3 A, the peak inductor current is 3.21 A, and the inductor ripple current is 0.41 A. The selected inductor is a Coilcraft XAL4030-332ME, which has a saturation-current rating of 5.5 A and an RMS-current rating of 5 A. As the equation set demonstrates, lower ripple current reduces the output ripple voltage of the buck regulator but requires a larger value of inductance. Selecting higher ripple currents increases the output ripple voltage of the buck regulator but allows for a lower inductance value.
8.2.1.2.3 Output Capacitor Selection for the Buck Regulator
Consider three primary factors when selecting the value of the output capacitor. The output capacitor determines the modulator pole, the output ripple voltage, and how the buck regulator responds to a large change in load current. Select the output capacitance based on the most stringent of these three criteria. The desired response to a large change in the load current is the first criterion. The output capacitor must supply the load with current when the regulator cannot. This situation occurs if the desired hold-up times are present for the buck regulator. In this case, the output capacitor must hold the output voltage above a certain level for a specified amount of time after the input power is removed. The regulator is also temporarily unable to supply sufficient output current if a large, fast increase occurs affecting the current requirements of the load, such as a transition from no load to full load. The buck regulator usually requires two or more clock cycles for the control loop to notice the change in load current and output voltage, and to adjust the duty cycle to react to the change. Size the output capacitor to supply the extra current to the load until the control loop responds to the load change. The output capacitance must be large enough to supply the difference in current for two clock cycles while only allowing a tolerable amount of droop in the output voltage. Use Equation 27 to calculate the minimum output capacitance required to supply the difference in current.
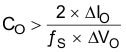
where
- ΔIO is the change in the buck-regulator output current
- ƒS is the switching frequency of the buck regulator
- ΔVO is the allowable change in the buck-regulator output voltage
For this example, the specified transient load response is a 3% change in VO for a load step from 0.01 A to 0.8 A. For this example, ΔIO = 0.8 – 0.01 = 0.79 A and ΔVO = 0.03 × 3.3 = 0.1 V. Using these numbers results in a minimum capacitance of 7.2 µF. This value does not consider the ESR of the output capacitor in the output voltage change. For ceramic capacitors, the ESR is usually small enough to ignore in this calculation. Aluminum electrolytic and tantalum capacitors have higher ESR that must be take into consideration.
The catch diode of the regulator cannot sink current. Therefore any stored energy in the inductor produces an output-voltage overshoot when the load current rapidly decreases. Also, size the output capacitor to absorb the energy stored in the inductor when transitioning from a high load current to a lower load current. The excess energy that is stored in the output capacitor increases the voltage on the capacitor. Size the capacitor to maintain the desired output voltage during these transient periods.
Use Equation 28 to calculate the minimum capacitance to keep the output voltage overshoot to a desired value.
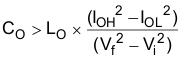
where
- LO is the output inductance of the buck regulator
- IOH is the output current of the buck regulator under heavy load
- IOL is the output current of the buck regulator under light load
- Vf is the final peak output voltage of the buck regulator
- Vi is the initial capacitor voltage of the buck regulator
For this example, the worst-case load step is from 3 A to 0.01 A. The output voltage increases during this load transition, and the stated maximum in the specification is 3% of the output voltage (see the Electrical Characteristics table). This makes Vf = 1.03 × 3.3 = 3.4 Vi is the initial capacitor voltage, which is the nominal output voltage of 3.3 V. Using these numbers in Equation 28 yields a minimum capacitance of 30 µF.
Equation 29 calculates the minimum output capacitance needed to meet the output ripple-voltage specification. Equation 29 yields 0.8 µF.
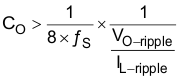
where
- VO-ripple is the maximum allowable output ripple voltage of the buck regulator
- IL-ripple is the inductor ripple current of the buck regulator
Use Equation 30 to calculate the maximum ESR required for the output capacitor to meet the output voltage ripple specification. As a result of Equation 30, the ESR should be less than 80 mΩ.
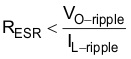
The most stringent criterion for the output capacitor is 30 µF of capacitance to keep the output voltage in regulation during a load transient.
Factor in additional capacitance deratings for aging, temperature, and DC bias which increase this minimum value. For this example, two 47-µF, 25-V ceramic capacitors with 3 mΩ of ESR are used (see C4 and C5 in Figure 20). Capacitors generally have limits to the amount of ripple current they can handle without failing or producing excess heat. Specify an output capacitor that can support the inductor ripple current. Some capacitor data sheets specify the root-mean-square (RMS) value of the maximum ripple current.
Use Equation 31 to calculate the RMS ripple current that the output capacitor must support. For this application, Equation 31 yields 119 mA.
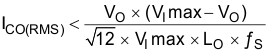
8.2.1.2.4 Catch Diode Selection for the Buck Regulator
The TPS65321-Q1 device requires an external catch diode between the SW pin and GND (see D1 in Figure 20). The selected diode must have a reverse voltage rating equal to or greater than VImax. The peak current rating of the diode must be greater than the maximum inductor current. The diode should also have a low forward voltage. Schottky diodes are typically a good choice for the catch diode because of low forward voltage of these diodes. The lower the forward voltage of the diode, the higher the efficiency of the regulator.
Typically, the higher the voltage and current ratings the diode has, the higher the forward voltage is. Although the design example has an input voltage up to 36 V, select a diode with a minimum of 40-V reverse voltage to allow input voltage transients up to the rated voltage of the TPS65321-Q1 device.
For the example design, the selection of a Schottky diode is SL44-E3/57 based on the low forward voltage of this diode. This diode is also available in a larger package size, which has better thermal characteristics. The typical forward voltage of the SL44-E3/57 is 0.44 V.
Also, select a diode with an appropriate power rating. The diode conducts the output current during the off-time of the internal power switch. The off-time of the internal switch is a function of the maximum input voltage, the output voltage, and the switching frequency. The output current during the off-time, multiplied by the forward voltage of the diode, equals the conduction losses of the diode. At higher switching frequencies, consider the AC losses of the diode. The AC losses of the diode are because the charging and discharging of the junction capacitance and reverse recovery.
8.2.1.2.5 Input Capacitor Selection for the Buck Regulator
The TPS65321-Q1 device requires a high-quality ceramic input decoupling capacitor (type X5R or X7R) of at least 3 µF of effective capacitance, and in some applications a bulk capacitance. The effective capacitance includes any DC bias effects. The voltage rating of the input capacitor must be greater than the maximum input voltage. The capacitor must also have a ripple-current rating greater than the maximum input-current ripple of the TPS65321-Q1 device. Use Equation 32 to calculate the input ripple current (ICI(RMS)).
The value of a ceramic capacitor varies significantly over temperature and the amount of DC bias applied to the capacitor. Minimize the capacitance variations because of temperature by selecting a dielectric material that is stable over temperature. Designers usually select X5R and X7R ceramic dielectrics for power regulator capacitors because these capacitors have a high capacitance-to-volume ratio and are fairly stable over temperature. Also, select the output capacitor with the DC bias taken into consideration. The capacitance value of a capacitor decreases as the DC bias across a capacitor increases.
This design requires a capacitor with at least a 40-V voltage rating to support the maximum input voltage. Common standard capacitor voltage ratings include 4 V, 6.3 V, 10 V, 16 V, 25 V, 50 V, 63V, or 100 V. For this design example. The selection for this example is a 100-µF, 50-V capacitor (see C8 in Figure 20).
The input-capacitance value determines the input ripple voltage of the regulator. Use Equation 33 to calculate the input ripple voltage (ΔVI).
Using the design example values, IOmax = 3 A, CI = 100 µF, ƒS = 2200 kHz, yields an input ripple voltage of 3.4 mV and an RMS input ripple current of 1.49 A.
8.2.1.2.6 Soft-Start Capacitor Selection for the Buck Regulator
The soft-start capacitor determines the minimum amount of time required for the output voltage to reach the nominal programmed value during power up which is useful if a load requires a controlled-voltage slew rate. This feature is also useful if the output capacitance is large and requires large amounts of current to charge the capacitor quickly to the output voltage level. The large currents required to charge the capacitor may make the TPS65321-Q1 device reach the current limit, or excessive current draw from the input power supply may cause the input voltage rail to sag. Limiting the output voltage-slew rate solves both of these problems.
The soft-start time must be long enough to allow the regulator to charge the output capacitor up to the output voltage without drawing excessive current. Use Equation 34 to calculate the minimum soft-start time, tss, required to charge the output capacitor, CO, from 10% to 90% of the output voltage, VO, with an average load current of Io(avg).
In the example, to charge the effective output capacitance of 94 µF up to 3.3 V while allowing the average output current to be 3 A requires a 0.083 ms soft-start time.
When the soft-start time is known, use Equation 2 to calculate the soft-start capacitor. For the example circuit, the soft-start time is not too critical because the output-capacitor value is 2 × 47 µF, which does not require much current to charge to 3.3 V. The example circuit has the soft-start time set to an arbitrary value of 1 ms, which requires a 3.125 nF soft-start capacitor. This design uses the next-larger standard value of 3.3 nF.
8.2.1.2.7 Bootstrap Capacitor Selection for the Buck Regulator
Connect a 0.1-µF ceramic capacitor between the BOOT and SW pins for proper operation. TI recommends using a ceramic capacitor with X5R or better-grade dielectric. The capacitor should have a 10-V or higher voltage rating.
8.2.1.2.8 Output Voltage and Feedback Resistor Selection for the Buck Regulator
The voltage divider of R1 and R2 sets the output voltage. For the design example, the selected value of R2 is 10 kΩ, and the calculated value of R1 is 32.1 kΩ. Because of current leakage of the FB1 pin, the current flowing through the feedback network should be greater than 1 μA to maintain the output-voltage accuracy. Selecting higher resistor values decreases the quiescent current and improves efficiency at low output currents, but can introduce noise immunity problems.
8.2.1.2.9 Frequency Compensation Selection for the Buck Regulator
Several possible methods exist to design closed loop compensation for DC-DC converters. The method presented here is easy to calculate and ignores the effects of the slope compensation that is internal to the buck regulator. Ignoring the slope compensation usually causes the actual crossover frequency to be lower than the crossover frequency used in the calculations. This method assumes the crossover frequency is between the modulator pole and the ESR zero, and that the ESR zero is at least 10 times greater than the modulator pole.
To begin, use Equation 35 to calculate the modulator pole, ƒP_mod, and Equation 36 to calculate the ESR zero, ƒz_mod.
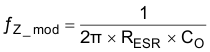
Use Equation 37 and Equation 38 to calculate an estimate starting point for the crossover frequency, ƒCO, to design the compensation.

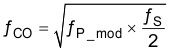
For the example design, ƒP_mod is 1.54 kHz and ƒZ_mod is 564 kHz. Equation 37 is the geometric mean of the modulator pole and the ESR zero and Equation 38 is the mean of the modulator pole and the switching frequency. Equation 37 yields 29.5 kHz and Equation 38 results 41.1 kHz. Use the lower value of Equation 37 or Equation 38 for an initial crossover frequency.
For this example, the target ƒCO value is 29.5 kHz. Next, calculate the compensation components. Use a resistor in series with a capacitor to create a compensating zero. A capacitor in parallel to these two components forms the compensating pole.
The total loop gain, which consists of the product of the modulator gain, the feedback voltage-divider gain, and the error amplifier gain at ƒCO equal to 1. Use Equation 39 to calculate the compensation resistor, R3 (see the schematic in Figure 20).
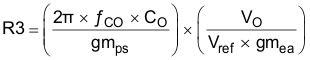
Assume the power-stage transconductance, gmps, is 10.5 S. The output voltage (VO), reference voltage (Vref), and amplifier transconductance, (gmea) are 3.3 V, 0.8 V, and 310 μS, respectively. The calculated value for R3 is 22.1 kΩ. For this design, use a value of 22 kΩ for R3. Use Equation 40 to set the compensation zero to the modulator pole frequency.
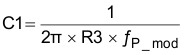
Equation 38 yields 4.69 nF for compensating capacitor C1 (see the schematic in Figure 20). For this design, select a value of 4.7 nF for C1.
To implement a compensation pole as needed, use an additional capacitor, C2, in parallel with the series combination of R3 and C1. Use Equation 41 and Equation 42 to calculate the value of C2 and select the larger resulting value to set the compensation pole. Type 2B compensation does not use C2 because it would demand a low ESR of the output capacitor.
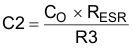
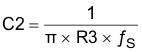
8.2.1.2.10 LDO Regulator
Depending on the end application, use different values of external components can be used. To program the output voltage, carefully select the feedback resistors, R5 and R6 (see the schematic in Figure 20). Using smaller resistors results in higher current consumption, whereas using very large resistors impacts the sensitivity of the regulator. Therefore selecting feedback resistors such that the sum of R5 and R6 is between 20 kΩ and 200 kΩ is recommended.
If the desired regulated output voltage is 5 V on selecting R6, the value of R5 can be calculated. With Vref = 0.8 V (typical), VO = 5 V, and selecting R6 = 18 kΩ, the calculated value of R5 is 95.3 kΩ.
An output capacitor for the LDO regulator is required (see C10 in Figure 20) to prevent the output from temporarily dropping down during fast load steps. TI recommends a low-ESR ceramic capacitor with dielectric of type X5R or X7R. Additionally, a bypass capacitor can be connected at the output to decouple high-frequency noise based on the requirements of the end application.
8.2.1.2.11 Power Dissipation
8.2.1.2.11.1 Power Dissipation Losses of the Buck Regulator
Use the following equations to calculate the power dissipation losses for the buck regulator. These losses are applicable for continuous-conduction-mode (CCM) operation.
- Conduction loss:
- IO is the buck regulator output current
- VO is the buck regulator output voltage
- VI is the input voltage
- Switching loss:
- tr is the FET switching rise time (tr maximum = 20 ns)
- tf is the FET switching fall time (tf maximum = 20 ns)
- ƒS is the switching frequency of the buck regulator
- Gate drive loss:
- Vdrive is the FET gate-drive voltage (typically Vdrive = 6 V)
- Qg = 1 × 10–9 (nC, typical)
where
where
where
8.2.1.2.12 Power Dissipation Losses of the LDO Regulator
8.2.1.2.13 Total Device Power Dissipation Losses and Junction Temperature
- Supply loss:
- Total power loss:
For a given operating ambient temperature TA:
where
- TJ is the junction temperature in °C
- TA is the ambient temperature in °C
- Rth is the thermal resistance of package in (°C/W)
- PTotal is the total power dissipation (W)
For a given maximum junction temperature TJ-max = 150°C, the allowed Total power dissipation is given as:
where
- TA-max is the maximum ambient temperature in °C
- TJ-max is the maximum junction temperature in °C
Additional power losses occur in the regulator circuit because of the inductor AC and DC losses, the Schottky diode, and trace resistance that impact the overall efficiency of the regulator.
Figure 21 shows the thermal derating profile of the 14-pin HTSSOP Package With PowerPAD™ . It is important to consider additional cooling strategies if necessary to maintain the junction temperature of the device below the maximum junction temperature of 150 °C.
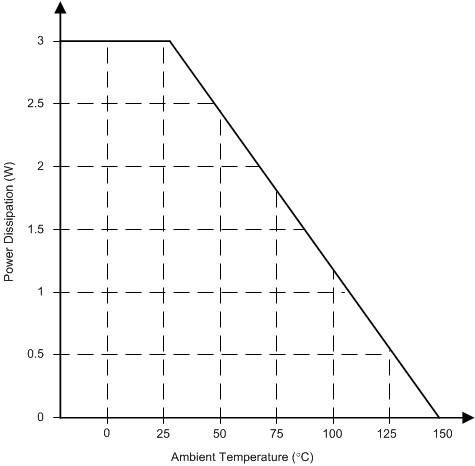 Figure 21. Thermal Derating Profile ofTPS65321-Q1 in 14-pin HTSSOP Package With PowerPAD
Figure 21. Thermal Derating Profile ofTPS65321-Q1 in 14-pin HTSSOP Package With PowerPAD
8.2.1.3 Application Curves
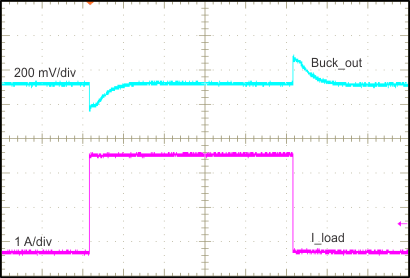
| 100 µs/div | ƒS = 2 MHz | Buck Output Voltage = 5 V |
(200 mA to 3 A)
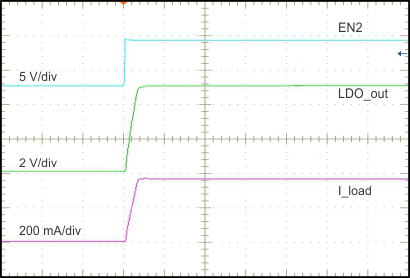
| 400 µs/div |
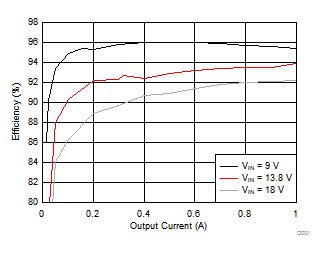
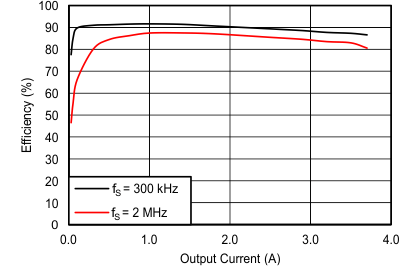 Figure 26. Buck Efficiency Versus Output Current
Figure 26. Buck Efficiency Versus Output Current
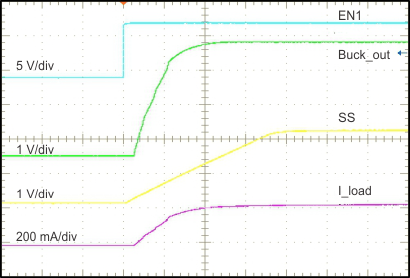
| 1 ms/div |
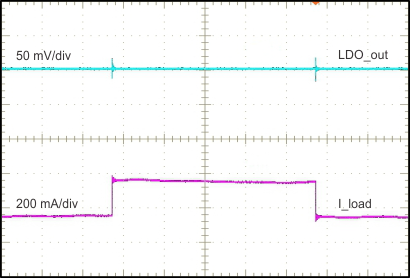
| 10 µs/div | V(LDO_OUT) = 5 V |
(50 mA to 300 mA)
8.2.2 Design Example With 500-kHz Switching Frequency
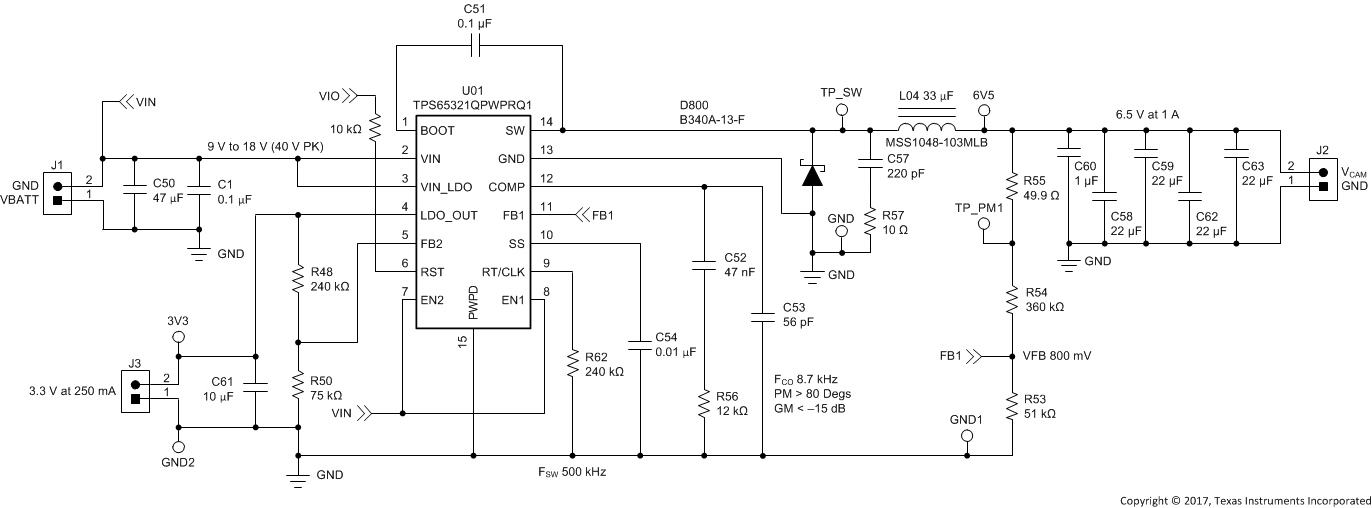
8.2.2.1 Design Requirements
This example begins with the parameters listed in Table 4.
Table 4. Design Parameters
| DESIGN PARAMETER | EXAMPLE VALUE |
|---|---|
| Input voltage, VIN1 | 9 V to 18 V, typical 12 V |
| Output voltage, VREG1 (buck regulator) | 6.5 V ± 2% |
| Maximum output current IO_max1 | 1 A |
| Minimum output current IO_min1 | 0.01 A |
| Transient response 0.01 A to 1 A | 3% |
| Output ripple voltage | 1% |
| Switching frequency ƒSW | 500 kHz |
| Output voltage, VREG2 (LDO regulator) | 3.3 V ± 2% |
| Overvoltage threshold | 106% of output voltage |
| Undervoltage threshold | 91% of output voltage |
8.2.2.2 Detailed Design Procedure
For the 500-kHz switching-frequency design, make the adjustments as outlined in the following sections. For sections such as LDO-component calculations, bootstrap-capacitor selection, and others that are not listed in this section, see the 2.2-MHzSwitching Frequency, 9-V to 16-V Input, 3.3-V Output Buck Regulator, 5-V Output LDO Regulator section.
8.2.2.2.1 Selecting the Switching Frequency
For 500-kHz operation, use a 240-kΩ resistor which is calculated using Equation 3. The R62 resistor sets this switching frequency.
8.2.2.2.2 Output Inductor Selection
Using Equation 23, the inductor value is calculated as 27.7 μH with KIND = 0.3. This design example can allow for a higher ripple current, therefore, select the nearest standard value of 33 µH. The RMS and peak inductor-current ratings are calculated using Equation 25 and Equation 26 which result in 1.00 A and 1.13 A, respectively. The value of the output-filter inductor must not exceed the RMS-current and saturation-current ratings.
8.2.2.2.3 Output Capacitor
For this example, the specified transient load response is a 3% change in VO for a load step from 0.01 A to 1 A (full load). For this example, ΔIO = 1 – 0.01 = 0.99 A and ΔVO = 0.03 × 6.5 = 0.195 V. Using these numbers results in a minimum capacitance of 20.31 μF. This value does not consider the ESR of the output capacitor in the output voltage change. For ceramic capacitors, the ESR is usually small enough to ignore in this calculation.
Aluminum electrolytic and tantalum capacitors have higher ESR that should be considered. The catch diode of the regulator cannot sink current, so any stored energy in the inductor produces an output-voltage overshoot when the load current rapidly decreases. Also, size the output capacitor to absorb the energy stored in the inductor when transitioning from a high load current to a lower load current. The excess energy that is stored in the output capacitor increases the voltage on the capacitor. Size the capacitor to maintain the desired output voltage during these transient periods. Use Equation 28 to calculate the minimum capacitance to keep the output voltage overshoot to a desired value.
For this example, the worst-case load step is from 1 A to 0.01 A. The output voltage increases during this load transition, and the stated maximum in our specification is 3% of the output voltage resulting in Vf = 1.03 × 6.5 = 6.7. The initial capacitor voltage, Vi, is the nominal output voltage of 5 V. Using these values, Equation 28 yields a minimum capacitance of 3.88 μF. Equation 29 calculates the minimum output capacitance required to meet the output ripple-voltage specification. Equation 29 yields 10.6 μF. Equation 30 calculates the maximum ESR an output capacitor can have to meet the output ripple-voltage specification. Equation 30 indicates the ESR should be less than 60.2 mΩ.
The most stringent criterion for the output capacitor is 20.31 μF of capacitance to keep the output voltage in regulation during a load transient.
Factor in additional capacitance deratings for aging, temperature, and DC bias which increase this minimum value. For this example, four 22-μF, 25-V and one 1-µF, 25-V ceramic capacitors with 10 mΩ of ESR are used. Specify an output capacitor that can support the inductor ripple current. Some capacitor data sheets specify the RMS value of the maximum ripple current. Use Equation 31 to calculate the RMS ripple current that the output capacitor must support. For this design example, Equation 31 yields 240 mA.
8.2.2.2.4 Compensation
This design example use a different approach for calculating compensation values, beginning with the desired crossover frequency. Ensure that the crossover frequency is maintained at 10 kHz to provide reasonable phase margin (PM). To achieve circuit stability, a phase margin greater than 60 degrees and a gain margin less than 15 dB is required. Next, place the zero close to the load pole. The zero is determined using C52 and R56. For this example, select a value of 10 kΩ for R56 which results in a value of approximately 4.7 nF for C52. The pole, resulting from C53 and R56, can be placed between 10 times the crossover frequency and 1/3 of the switching frequency. The gain is adjusted to be maintained over 60 degrees of phase margin and –15 dB of gain margin. The resulting value of C53 is approximately 100 pF for a pole frequency of 159 kHz.
Use the following component values:
R56 = 12 kΩ
C53 = 56 pF
C52 = 47 nF
8.2.2.3 Application Curve