There are several considerations in determining the value of the output capacitor. The selection of the output capacitor is driven by both the desired output voltage ripple and the allowable voltage deviation due to a large and abrupt change in load current. For space applications, the value of capacitance also has to account for the mitigation of single event effects (SEE). The output capacitance needs to be selected based on the more stringent of these three criteria. It is also important to note that the value of the output capacitor directly influences the modulator pole of the converter frequency response, as shown in Small Signal Model for Frequency Compensation.

The desired response to a large change in the load current is the first criteria. The output capacitor needs to supply the load with current when the regulator can not. This situation would occur if there are desired hold-up times for the regulator where the output capacitor must hold the output voltage above a certain level for a specified amount of time after the input power is removed. The regulator is also temporarily not able to supply sufficient output current if there is a large, fast increase in the current needs of the load such as a transition from no load to full load. The output capacitor must be sized to supply the extra current to the load until the control loop responds to the load change. Equation 27 shows the minimum output capacitance, from the electrical point of view, necessary to accomplish this.

Equation 27.

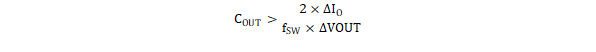
Where ΔI_O is the change in output current, f_SW is the regulator switching frequency, and ΔVOUT is the allowable change in the output voltage. For this example, the transient load response is specified as a 5% change in VOUT for a load step of 9 A. Also in this example, ΔI_O = 9 A and ΔVOUT = 0.05 × 1 = 0.05 V. Using these numbers gives a minimum capacitance of 720 μF. This value does not take the ESR of the output capacitor into account in the output voltage change. For ceramic capacitors, the ESR is usually small enough to ignore in this calculation. However, for space applications and large capacitance values, tantalum capacitors are typically used, which have a certain ESR value to take into consideration.

Equation 28 calculates the minimum output capacitance needed to meet the output voltage ripple specification. Where f_SW is the switching frequency, VOUT_ripple is the maximum allowable output voltage ripple, and I_ripple is the inductor ripple current. In this case, the maximum output voltage ripple is 20 mV and the inductor ripple current is 1.8 A. Under these conditions, Equation 28 yields 22.5 µF.

Equation 28.

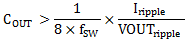
Additional capacitance de-ratings for aging, temperature and DC bias should be factored in, which increases this minimum value. Capacitors generally have limits to the amount of ripple current they can handle without failing or producing excess heat. An output capacitor that can support the inductor ripple current must be specified. Some capacitor data sheets specify the RMS (Root Mean Square) value of the maximum ripple current. Equation 25 can be used to calculate the RMS ripple current the output capacitor needs to support. For this application, Equation 25 yields 519 mA.

Equation 29 calculates the maximum ESR an output capacitor can have to meet the output voltage ripple specification. Equation 29 indicates the ESR should be less than 11.11 mΩ.

Equation 29.

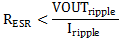
For this specific design, taking into consideration the stringent requirements for space applications, a total output capacitance of 2 mF with an equivalent ESR of approximately 2 mΩ has been selected.