The immediate solution to the above problem is to isolate this capacitance from the output node of the amplifier via additional resistance. The interactions between the output impedance of the amplifier and this RC network are discussed in Output Filter Discussion and Design, but it is beneficial to explore the nature of this filter as it relates to the ADC input stage. Examining the voltage on the filter capacitor, recall that for a typical RC network in the time domain, the voltage charges as a function of the RC time constant, given as

Equation 8.

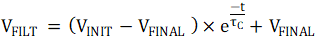
where V_INIT is the initial charge on the filter capacitor prior to the beginning of the sample and hold cycle, V_FINAL is the final voltage that the capacitor charges to, and τ_C is the total time constant for the system with which the node will charge that includes contributions from both the RC network as well as the amplifier. The addition of resistance on the output reduces the amount of the current that can be delivered by the amplifier, and also filters higher frequency components of the signal based on the cutoff frequency formed by the RC response with C_FILT. The goal then, is to ensure that for the given C_FILT, the system is still able to settle to within 1/2 LSB within the sample and hold cycle of the ADC. For the above expression, this equates to

Equation 9.

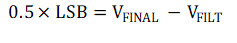
It can also be observed that the maximum magnitude between V_INIT and V_FINAL is simply V_DROOP, or

Equation 10.

Rearranging and substituing these into the RC equation, it can then be expressed that

Equation 11.

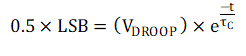
Solving this expression for τ_C, the relationship of V_FILT is then expressed in terms of settling as

Equation 12.

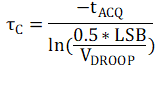
However, since the CSA also contributes to this charge, an expression relating τ_C to both of these is needed. Since the CSA is approximated as a second order system, the shared contribution of both of these can be approximated using an root-mean-square (RMS) approach, or

Equation 13.

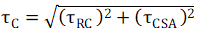
And given the assumption that the CSA is 4 times as fast as the RC network,

Equation 14.

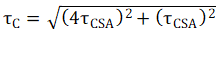
Solving this equation for τ_CSA yields

Equation 15.

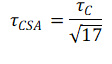
And substituting this back into the relationship for the RC time constant gives

Equation 16.

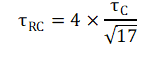
This approximation again allows the rendering of a ratiometric relationship between the RC network, the CSA, and the total network allowing the system to be solved. R_FILT is then given as

Equation 17.

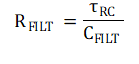
However, given the nature of the approximations above, an optimal value of R_FILT may fluctuate slightly from this calculated value, so a range of values is examined, typically from 0.25*R_FILT < R_FILT < 2*R_FILT.

Finally, with values for R_FILT and C_FILT determined, the bandwidth needed by the amplifier can be determined. Expressing the bandwidth of the amplifier in terms of frequency, and relating this to the RC time constant, this is given as

Equation 18.

This reveals that if the bandwidth determined here is greater than the bandwidth of the current amplifier, adjustments must be made to ensure accurate settling.