As previously mentioned, Keyexpansion refers to the process in which the 128 bits of the original key are expanded into eleven 128-bit round keys.

To compute round key (n+1) from round key (n) these steps are performed:

1. Compute the new first column of the next round key as shown in Figure 4-7:
   Figure 4-7 Expanding First Column of Next Round Key

   First, all bytes of the old fourth column must be substituted using the Subbytes operation. These four bytes are shifted vertically by one byte position and then XORed to the old first column. The result of these operations is the new first column.

2. Calculate columns 2 to 4 of the new round key as shown:
   1. [new second column] = [new first column] XOR [old second column]
   2. [new third column] = [new second column] XOR [old third column]
   3. [new fourth column] = [new third column] XOR [old fourth column]

   Figure 4-8 illustrates the calculation of columns 2 to 4 of the new round key.

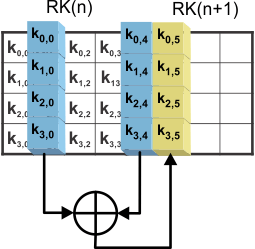   Figure 4-8 Expanding Other Columns of Next Round Key