Probably the most complex operation from a software implementation perspective is the Mixcolumns step. The working method of Mixcolumns can be seen in Figure 4-5.

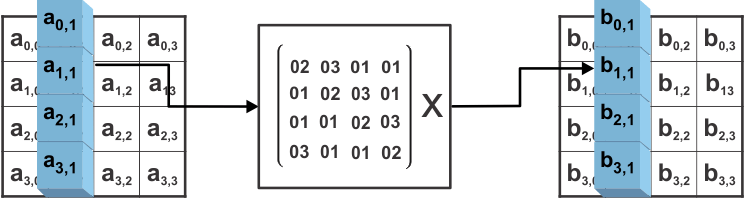Figure 4-5 Mixcolumns Operation

Opposed to the Shiftrows operation, which works on rows in the 4x4 state matrix, the Mixcolumns operation processes columns.

In principle, only a matrix multiplication needs to be executed. To make this operation reversible, the usual addition and multiplication are not used. In AES, Galois field operations are used. This document does not go into the mathematical details, it is only important to know that in a Galois field, an addition corresponds to an XOR and a multiplication to a more complex equivalent.

The fact that there are many instances of 01 in the multiplication matrix of the Mixcolumns operation makes this step easily computable.