2 Understanding the Thermal Flow

The equation used for calculating the thermal dissipation of a system is shown in Equation 1:

Where:

• θ_JA = thermal resistance
• T_J = junction temperature
• T_A = ambient temperature
• P_D = power dissipation

θ_JA represents the thermal resistance path(s) where the heat will flow out of the amplifier to relatively cooler surroundings. There are two paths where the heat generated from the device can go. As seen in Figure 2-1, for top-mounted heatsinks, heat can escape from the junction to the thermal pad (case), then to the thermal interface material. From the thermal interface material the heat goes to the heatsink, then through the heatsink to the surrounding air. The second path is from the junction to the board, then from the board to surrounding air.

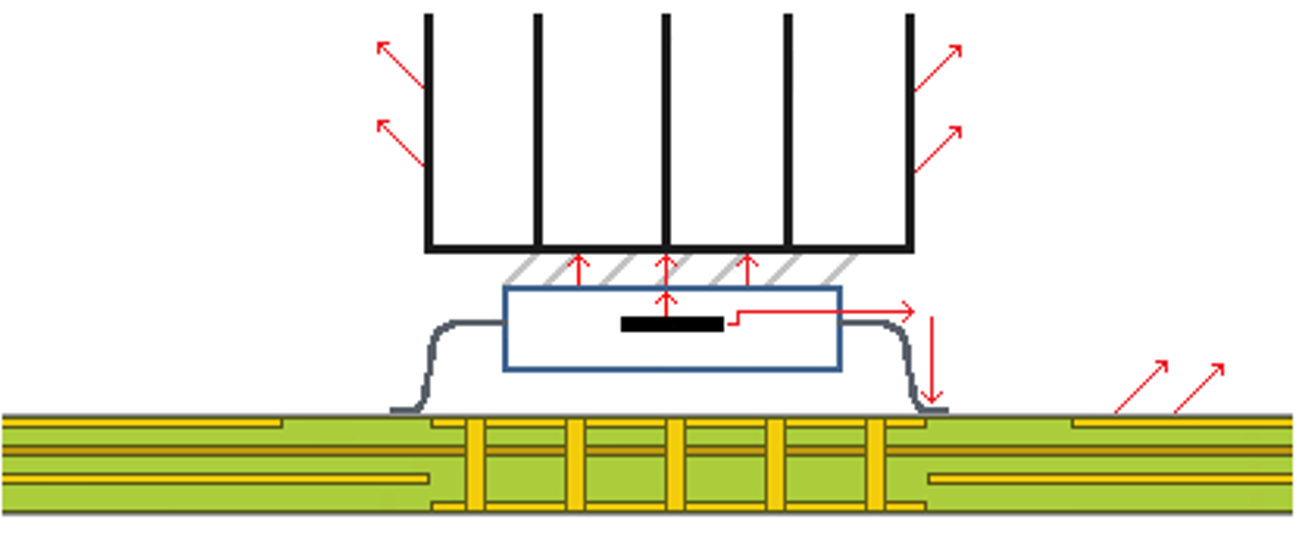Figure 2-1 Thermal Model

Using thermal dissipation equations, the thermal model seen in Figure 2-1 can be represented as shown in Figure 2-2 where:

• θ_JC = thermal resistance of the device from the junction to the case
• θ_CH = thermal resistance of the interface compound
• θ_HA = thermal resistance of the heatsink
• θ_JB = thermal resistance of the device from the junction to the board
• θ_BA = thermal resistance of the board

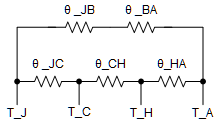Figure 2-2 Thermal Resistance Model

This can be simplified as the majority of the heat from the device will be going through the case into the heatsink rather than from the package to the board as θ_JC, θ_CH, and θ_HA have a much lower combined thermal resistance to that of θ_JB and θ_BA. The simplified thermal resistance model is shown in Figure 2-3.

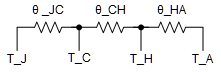Figure 2-3 Simplified Thermal Resistance Model

With the simplified thermal resistance model, the thermal dissipation equation can be written as:

Since θ_JC represents the intrinsic thermal properties between the junction and case of the device, it cannot be changed. θ_CH and θ_HA will vary greatly from system to system depending on the materials chosen for the heatsink, weight and shape of the heatsink, thickness of the thermal gap filler, and the thermal resistance of the thermal gap filler.