SLAU367P October 2012 – April 2020 MSP430FR5041 , MSP430FR5043 , MSP430FR50431 , MSP430FR5847 , MSP430FR58471 , MSP430FR5848 , MSP430FR5849 , MSP430FR5857 , MSP430FR5858 , MSP430FR5859 , MSP430FR5867 , MSP430FR58671 , MSP430FR5868 , MSP430FR5869 , MSP430FR5870 , MSP430FR5872 , MSP430FR58721 , MSP430FR5887 , MSP430FR5888 , MSP430FR5889 , MSP430FR58891 , MSP430FR5922 , MSP430FR59221 , MSP430FR5947 , MSP430FR59471 , MSP430FR5948 , MSP430FR5949 , MSP430FR5957 , MSP430FR5958 , MSP430FR5959 , MSP430FR5962 , MSP430FR5964 , MSP430FR5967 , MSP430FR5968 , MSP430FR5969 , MSP430FR5969-SP , MSP430FR59691 , MSP430FR5970 , MSP430FR5972 , MSP430FR59721 , MSP430FR5986 , MSP430FR5987 , MSP430FR5988 , MSP430FR5989 , MSP430FR5989-EP , MSP430FR59891 , MSP430FR5992 , MSP430FR5994 , MSP430FR59941 , MSP430FR6005 , MSP430FR6007 , MSP430FR6035 , MSP430FR6037 , MSP430FR60371 , MSP430FR6041 , MSP430FR6043 , MSP430FR60431 , MSP430FR6045 , MSP430FR6047 , MSP430FR60471 , MSP430FR6820 , MSP430FR6822 , MSP430FR68221 , MSP430FR6870 , MSP430FR6872 , MSP430FR68721 , MSP430FR6877 , MSP430FR6879 , MSP430FR68791 , MSP430FR6887 , MSP430FR6888 , MSP430FR6889 , MSP430FR68891 , MSP430FR6920 , MSP430FR6922 , MSP430FR69221 , MSP430FR6927 , MSP430FR69271 , MSP430FR6928 , MSP430FR6970 , MSP430FR6972 , MSP430FR69721 , MSP430FR6977 , MSP430FR6979 , MSP430FR69791 , MSP430FR6987 , MSP430FR6988 , MSP430FR6989 , MSP430FR69891
37.2.8.3 Quadrature Decoding
The ESI can be used to decode quadrature-encoded signals. Signals that are 90° out of phase with each other are said to be in quadrature. To Create the signals, two sensors are positioned depending on the slotting, or coating of the encoder disk. Figure 37-20 shows two examples for the sensor positions and a quadrature-encoded signal waveform.
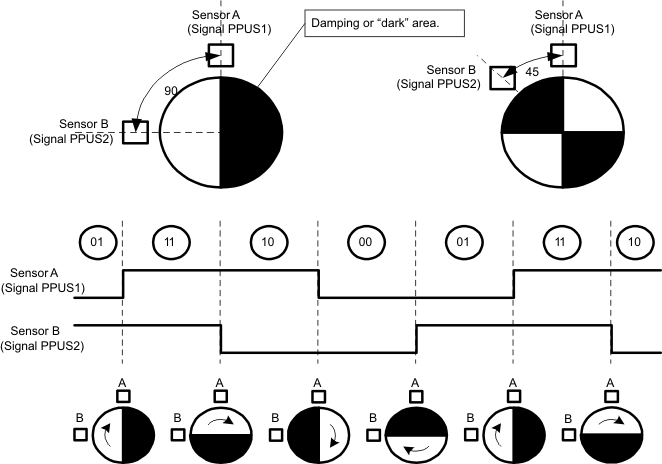Figure 37-20 Sensor Position and Quadrature Signals (S1=PPUS1, S2=PPUS2) Quadrature decoding requires knowing the previous quadrature pair S1 (PPUS1) and S2 (PPUS2), as well as the current pair. Comparing these two pairs will tell the direction of the rotation. For example, if the current pair is 00 it can change to 01 or 10, depending on direction. Any other change in the signal pair would represent an error as shown in Figure 37-21.
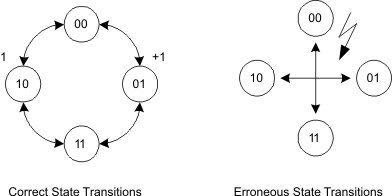Figure 37-21 Quadrature Decoding State Diagram To transfer the state encoding into counts it is necessary to decide what fraction of the rotation should be counted and on what state transitions. In this example only full rotations will be counted on the transition from state 00 to 01 or 10 using a 180° disk with the sensors 90° apart. All the possible state transitions can be put into a table and this table can be translated into the corresponding state table entries for the processing state machine as shown in Table 37-8.
Table 37-8 Quadrature Decoding PSM Table
| Previous Quadrature Pair | Current Quadrature Pair | Movement | State Table Entry | |||||
|---|---|---|---|---|---|---|---|---|
| Q6 | Q2 | Q1 | Q3 | Q0 | Byte Code | |||
| Error | -1 | +1 | Current Quadrature Pair | |||||
| 00 | 00 | No Rotation | 0 | 0 | 0 | 0 | 0 | 000h |
| 00 | 01 | Turns right, +1 | 0 | 0 | 1 | 0 | 1 | 003h |
| 00 | 10 | Turns left, -1 | 0 | 1 | 0 | 1 | 0 | 00Ch |
| 00 | 11 | Error | 1 | 0 | 0 | 1 | 1 | 049h |
| 01 | 00 | Turns left | 0 | 0 | 0 | 0 | 0 | 000h |
| 01 | 01 | No rotation | 0 | 0 | 0 | 0 | 1 | 001h |
| 01 | 10 | Error | 1 | 0 | 0 | 1 | 0 | 048h |
| 01 | 11 | Turns right | 0 | 0 | 0 | 1 | 1 | 009h |
| 10 | 00 | Turns right | 0 | 0 | 0 | 0 | 0 | 000h |
| 10 | 01 | Error | 1 | 0 | 0 | 0 | 1 | 041h |
| 10 | 10 | No rotation | 0 | 0 | 0 | 1 | 0 | 008h |
| 10 | 11 | Turns left | 0 | 0 | 0 | 1 | 1 | 009h |
| 11 | 00 | Error | 1 | 0 | 0 | 0 | 0 | 040h |
| 11 | 01 | Turns left | 0 | 0 | 0 | 0 | 1 | 001h |
| 11 | 10 | Turns right | 0 | 0 | 0 | 1 | 0 | 008h |
| 11 | 11 | No rotation | 0 | 0 | 0 | 1 | 1 | 009h |