SLOA313 May 2021 AFE7070 , AFE7071
2.6 Algorithm Calculations
The algorithm is essentially a series of linearly interpolated values based on the specific calibration points unique to each device and the temperature slopes characterized for the device at specific frequencies. The calibrated points are represented by (x1, y1) and (x2, y2). Note, there are actually three calibrated points, so choose the two points that encompass the actual frequency of operation. Variable y0 represents the new calibration parameter at frequency x0. First, calculate the adjusted value based on the frequency by interpolating between known calibration points.
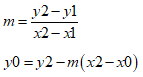
Next, calculate the temperature slope at the frequency of interest with the characterized slope per frequency as Table 2-1 shows.
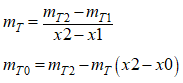
Finally, apply the temperature slope to derive an updated value at the frequency of interest.
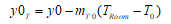
Equation 1 through Equation 2 consolidates into the following Python® code. The variable Fcal is an array with the calibrated frequency points. The variable DataCal is an array with the calibrated values and mTemp is the characterized temperature slopes. The ExtractCalPt function uses the array information to align with the specified frequency and temperature to calculate the adjusted parameter value.
def ExtractCalPt (Fcal, DataCal, mTemp, Freqi, Tempi) :
FDatai = int(round(np.interp(Freqi, Fcal, DataCal))) # Frequency adjustment
mi=np.interp(Freqi, Fcal, mTemp) # Temp slope at freq
FTDatai=int(round(mi*(Tempi - 25) + FDatai)) # Temp Adjustment
return(FTDatai)As an example, find the QMCP parameter at 140 MHz at –20°C given the following calibration points for the device: (136 MHz, 210) and (155 MHz, 157). Applying the calculations or executing the code yields a modified QMC-Phase parameter of 116.