3.2.2 Case 2: Large-signal Transient with Saturated Loop

In Case 2 (Figure 9), we assume that the control loop will go into partial or full saturation during transition period, the response of I_sum will be limited by the controller itself and circuit parameters. During a heavy transient, the voltage loop saturates and demands pulses as fast as possible, which means only blanking time will be between each rising edge of PWM pulse. This feature is helpful to high repetitive transient response, for example in short duration of load transient, all phases turn-on would generate too much energy and cause big overshoot. "Over-compensation" can be avoided by adding blanking time.

Blanking time prevents double pulsing of PWM, but at the same time limits the maximum capability of I_sum rising. Based on this feature, minimum per-phase switching period T_sat is limited to N*t_blank.

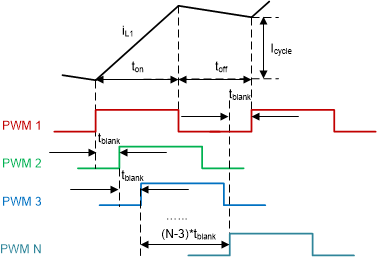Figure 9. Phase 1 Current I_L1 in Case 2

Looking into current I_L1 of phase 1 for example, shown in Figure 9. The effective switching cycle T_sat under saturation, and on/off time are calculated below:

Equation 10.

Equation 11.

Equation 12.

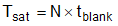
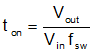
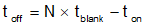
The effective current rising I_cycle in each phase, during one cycle is:

Equation 13.

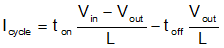
I_sum is rising with efforts of all phase current, during full loop saturation, representing the maximum ability of I_sum rising, this slew rate is:

Equation 14.

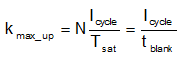
Loop delay time will become critical for undershoot and overshoot when loop is saturated. It means how much time needed for I_sum to respond to rising or falling I_o. This delay time is defined as t_{d_ud} and t_{d_ov} here, and affected by loop dynamic response, but typically 3 to 5 extra pulses if loop compensation is designed appropriately. Assume n_ex is number of extra pulses, we use t_{d_ud}/t_{d_ov}=n_ex*t_on to estimate roughly.

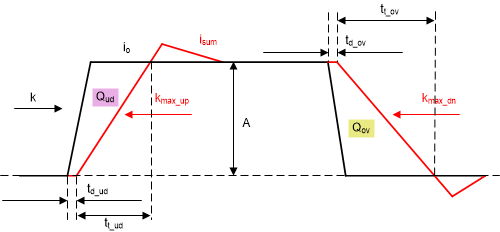Figure 10. Undershoot and Overshoot Calculation in Case 2

Figure 10 shows waveforms of how current difference contributes to undershoot and overshoot. With knowing I_cycle each cycle when current is rising, we can easily know how many cycles and also time duration, to make I_sum and I_o equal.

Equation 15.

Equation 16.

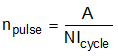
The discharges and undershoot are as follows:

Equation 17.

Equation 18.

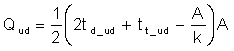
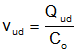
When I_sum is falling during full loop saturation, there is no pulse until steady state. Similarly, we have the following equations:

Equation 19.

Equation 20.

Equation 21.

Equation 22.

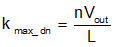
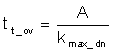
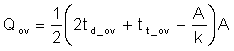
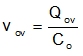
From formulas above, reducing inductance can surly lower undershoot/overshoot under saturated loop, but at the expense of efficiency with more current ripple. Also, when the loop is fully saturated, the output capacitance required will be affected by almost all the variations of load step characteristics, loop delay time, controller settings, and component parameters.