4 Existing Passive EMI Filtering Techniques

Figure 4-1 illustrates how to mitigate and filter EMI with passive components.

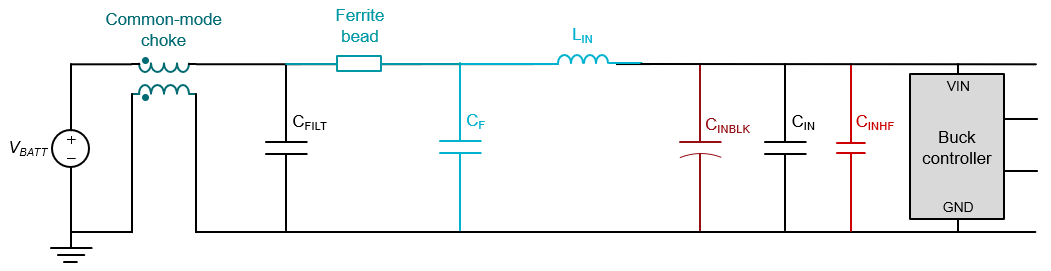Figure 4-1 Typical input filter components.

A high-frequency ceramic input capacitor helps supply the power metal-oxide semiconductor field-effect transistors (MOSFETs) with high-frequency energy to improve the switch’s slew-rate and edge characteristics, thus reducing switch ringing and high-frequency noise. Bulk capacitance provides low-frequency damping and prevents resonance between the filter components. A capacitor-inductor-capacitor (CLC) EMI filter, also known as a π filter, filters differential-mode noise from 10 MHz to 100 MHz, depending on the components selected.

Other components include a ferrite bead that provides high differential-mode impedance at very high frequencies. The ferrite bead impedance is typically specified at 100 MHz. A common-mode choke filters common-mode noise that usually occurs at high frequencies (10 MHz to 300 MHz).

Conventional CLC EMI filters use a capacitor and inductor arranged as a low-pass filter to attenuate noise from a noisy node to a quiet node. You can design the CLC components based on the required attenuation. Many tools are available to aid in designing filters, including application notes [2] and spreadsheet tools [3], as shown in Figure 4-2.

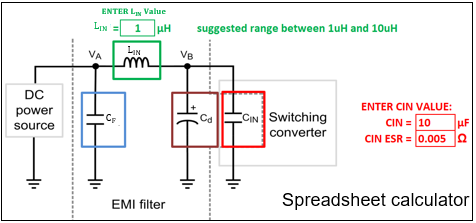Figure 4-2 Input filter calculator Excel tool for designing a CLC EMI filter.

Alternatively, you could use Equation 1 to measure or estimate the required attenuation:

where f_SW is the switching frequency, C_IN is the input capacitance, D is the duty cycle, I_DC is the converter-inductor DC current and V_MAX is the decibel microvolt (dBµV) limit at the switching frequency.

Looking again at Figure 4-2 and considering the filter inductor (L_IN) and filter capacitor (C_F), the CLC π filter provides 40 dB of attenuation per decade at frequencies above the cutoff frequency. Figure 3-1 takes the attenuation required at the switching frequency to design the π-filter cutoff frequency:

You can then use Equation 3 to select filter components based on the required cutoff frequency:

After selecting a typical L_IN range between 0.1 µH and 10 µH, you can calculate the required C_F value. Increasing the capacitance value – as opposed to using larger inductance values, since a larger inductance tends to increase the overall filter size – lowers the cutoff frequency. Plus, higher-value inductors tend to have decreased current ratings for a given size. The most space-efficient designs use more parallel capacitors rather than a larger inductor value.

Increasing C_F capacitance with multiple parallel capacitors is usually easier and more space-effective than increasing L_IN to adjust the filter cutoff frequency. Furthermore, a higher inductance will have a decreased current rating for given size.