SLYA042 July   2024 FDC1004 , FDC1004-Q1

 

  1.   1
  2.   Abstract
  3.   Trademarks
  4. 1 Introduction
  5. 2 CSAs and Input Bias Stage
  6. 3 CSA and Gain Error Factor
  7. 4 Applications for Resistance at Input Pins of Current Sense Amplifiers
    1. 4.1 Input Resistance Design Considerations
  8. 5 Applications for Input Resistance at Reference Pins of Current Sense Amplifiers
    1. 5.1 Bidirectional CSA and Applications
    2. 5.2 Driving CSA Reference Pin With High-Resistance Source Voltage
    3. 5.3 Input Resistance at Reference Pin Design Considerations
  9. 6 Design Procedure and Error Calculation for External Input Resistance on CSA
    1. 6.1 Calculating eEXT for INA185A4 With 110Ω Input Resistors
  10. 7 Design Procedure for Input Resistance on Capacitively-Coupled Current Sense Amplifier
    1. 7.1 Bench Verification of Input eEXT for Capacitively-Coupled Current Sense Amplifiers
  11. 8 Design Procedure for Input Resistance at CSA Reference Pins
  12. 9 Input Resistance Error Test with INA185 Over Temperature
    1. 9.1 Schematic
    2. 9.2 Methods
    3. 9.3 Theoretical Model
    4. 9.4 Data for INA185A4 with 110Ω Input Resistors
      1. 9.4.1 Data Calculations
    5. 9.5 Analysis
  13. 10Input Resistance Error Test with INA191 Over Temperature
    1. 10.1 Schematic
    2. 10.2 Methods
    3. 10.3 Theoretical Model
    4. 10.4 Data for INA191A4 With 2.2kΩ Input Resistors
      1. 10.4.1 Data Analysis
    5. 10.5 Analysis
  14. 11Derivation of VOS, EXT for a Single Stage Current Sense Amplifier (CSA)
  15. 12Summary
  16. 13References

3 CSA and Gain Error Factor

The typical device gain shown in data sheets for a single-stage, differential CSA is simply the matched ratio of RFB over RINT as shown in Equation 2.

Equation 2. G a i n t y p i c a l   =   R F B ,   t y p i c a l R I N T ,   t y p i c a l

When using input resistors (REXTERNAL or REXT), the total shunt voltage gain (GainTOTAL) becomes predictably attenuated due to a Gain Error Factor (GEF) that is less than 1. This new attenuated gain can be theoretically calculated using Equation 3. This total shunt voltage gain is now the new typical gain of the circuit. Note equations for a device's GEF are usually provided in data sheet.

Equation 3. G a i n T o t a l , t y p i c a l   =   G a i n t y p i c a l × G E F T y p i c a l

When introducing an input GEF, there is a new way to reference input offset voltages. Normally, the initial offset error specified in the data sheet (VOSI) is referred to the input (RTI), but to refer it to the shunt (RTS), you need to divide by the GEF. This also applies to the derivation of VOS, EXT RTI shown at end of document.

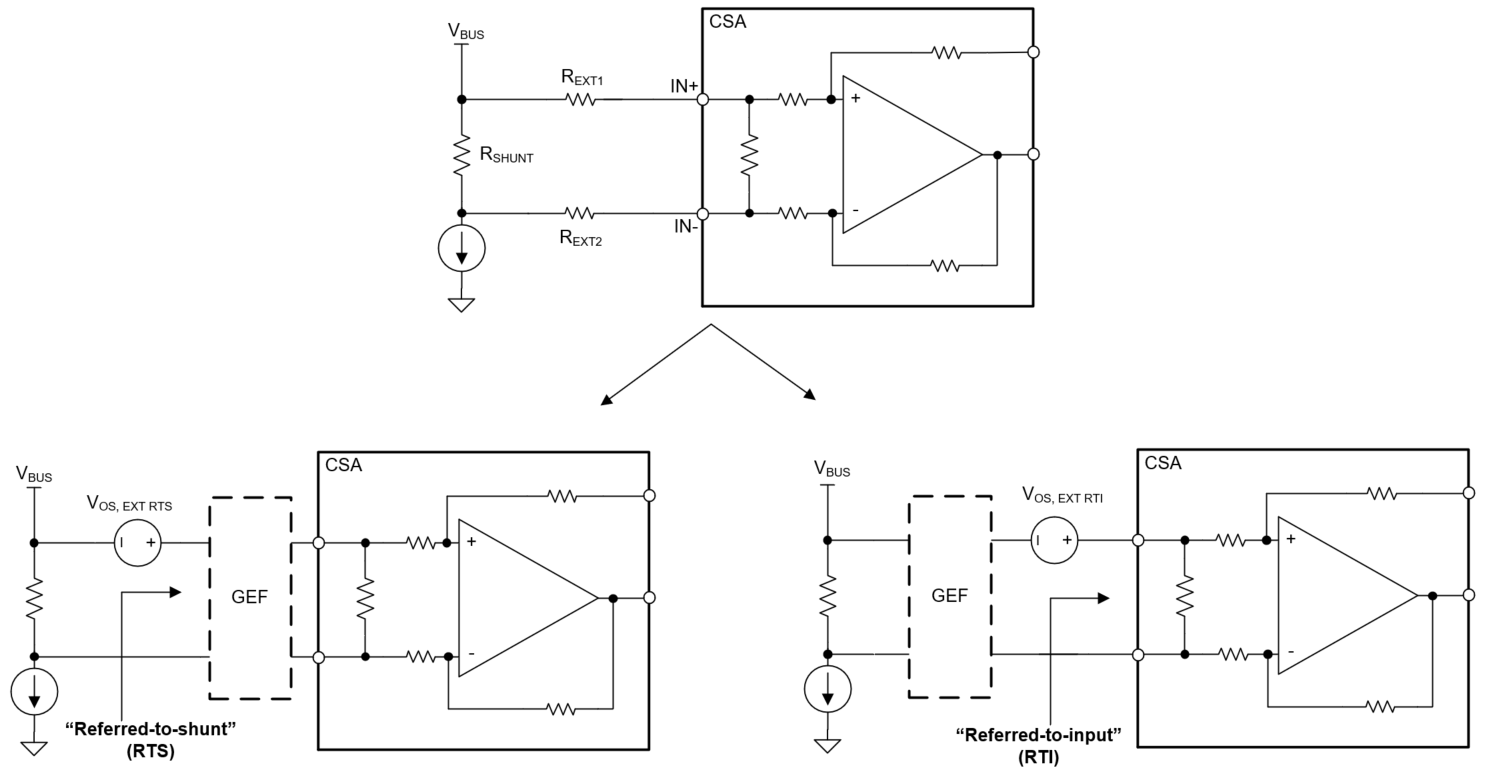RTI (Referred-to-input) and RTS (Referred-to-shunt) for CSA with Input Resistors Figure 3-1 RTI (Referred-to-input) and RTS (Referred-to-shunt) for CSA with Input Resistors
Equation 4. V O S   E X T   R T S   =   V O S   E X T   R T I G E F V O S I   R T S   =   V O S I   R T I G E F

Once the new typical total gain is determined, the designer can shift (calibrate) the shunt voltage gain in system hardware or software. However, there can be a significant increase in gain error variation (EG, EXT) over system population due to the fact that internal resistors are designed to achieve accurate ratios (Device Gain = RFB/RINT), not accurate absolute values.

For most CSAs, conservative evaluations put the absolute process variation (PV) of these resistors at ±20% and with temperature coefficients (PV_TC) of ±30 ppm/°C. These are based upon the specifications of the process technology. Furthermore, error analysis is simplified by the fact that all internal resistors for a single device can inherently have the same PV and PV_TC. With these PV specifications defined, a designer can calculate the bounds of external resistance loading error (eEXT).
千亿体育app官网登录(中国)官方网站IOS/安卓通用版/手机APP | 米乐app下载官网（中国）|ios|Android/通用版APP最新版 | 米乐|米乐·M6（中国大陆）官方网站 | 千亿体育登陆地址 | 华体会体育（中国）HTH·官方网站 | 千赢qy国际_全站最新版千赢qy国际V6.2.14安卓/IOS下载 | 18新利网v1.2.5|中国官方网站 | bob电竞真人（中国官网）安卓/ios苹果/电脑版【1.97.95版下载】 | 千亿体育app官方下载(中国)官方网站IOS/安卓/手机APP下载安装 |