Zachary Richards

In the previous post in this series, an equation was derived to describe the ratio of the Nth R_SET resistor in Figure 1 below.

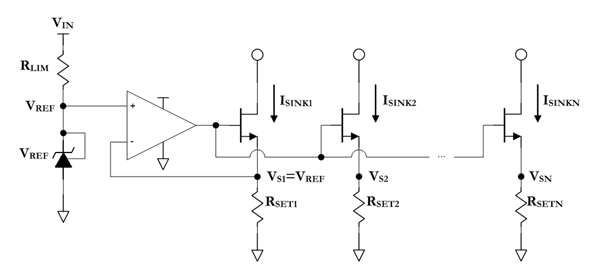Figure 1 Current Sink Network

That equation, again, is as follows:

So, what can be said about Equation 1? First of all, for an M_IN ratio of 1, the corresponding M_RN ratio will also be 1, as would be expected. Second, for values of M_IN greater than 1, notice that the two terms of the denominator of Equation 1 take on different signs. This means that depending on certain physical quantities involved (K_n, R_SET1, V_REF), M_RN can become arbitrarily large. Thus, this region should be avoided, instead favoring the M_IN ≤ 1 region; that is, by ensuring that I_SINKN is less than or equal to I_SINK1 for all N.

Notice that allowing the denominator of the root term in Equation 1 (the K_n, R_SET1, V_REF product) to become large results in a 1:1 linear relationship between M_RN and M_IN in the limit. Ultimately, the range of usable values that V_REF and R_SET1 can take on to increase this product are going to be limited by the headroom required for the sink; though it is worth noting that for a fixed I_SINK1 value, increasing V_REF requires an increase in R_SET1 as well. The final variable in the product, K_n, is the process transconductance of the MOSFET and can be maximized through device selection. The effect of K_n on the linearity of the M_RN, M_IN relationship (across five decades of K_n values) is illustrated in Figure 2 below.

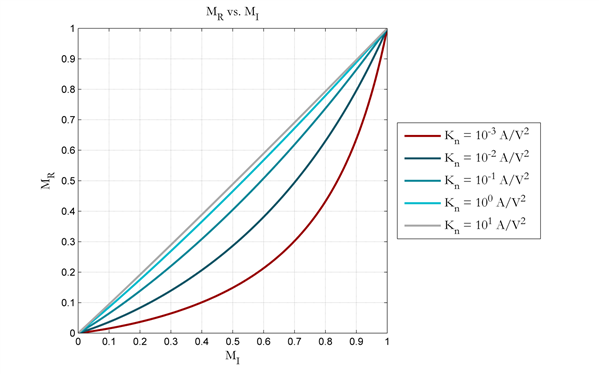Figure 2 Resistor Ratio vs. Current Ratio across Process Transconductance

The process transconductance is so named due to its dependence on carrier mobility, oxide permittivity, and oxide thickness (μ, ε_ox, t_ox)—all material and process properties:

However, it is also dependent on the W/L ratio of the device, so in general larger devices will result in increasingly linear behavior in Equation 1. While most datasheets will not include K_n, it can be calculated from a common datasheet parameter, the forward transconductance, often listed as g_m or g_FS:

Recall that the drain current equation for an NMOS operating in the saturation region is:

Neglecting channel length modulation and rewriting the terms of Equation 4:

This result can be substituted into Equation 3 and ultimately solved for K_n:

Thus, using Equation 7 it is possible to select optimal MOSFET devices for the bias network. Further, having obtained this value, it can be utilized in Equation 1 to calculate (more accurately) required R_SETN resistor values to produce desired I_SINKN currents.

It is important to note that Equation 1 tends to overestimate the R_SETN resistance in the M_IN ≤ 1 region; that is, it results in currents that are lower than the desired value. However, the ideal transistor case (M_IN=M_RN) will always underestimate the R_SETN resistance in this region. Thus, calculating these two values will ultimately bound the exact value required.  Consider two randomly chosen NFETs, N-channel MOSFET A  and N-channel MOSFET B, as represented in Table 1, which have listed g_FS values of 5.5A/V² (at I_D=9A) and 15A/V² (at I_D=31A), respectively. Suppose these are used to implement an M_IN ratio of ¼; the corrected R_SETN and M_RN ratios are calculated using Equation 1 (along with some straightforward design values) in Table 1 below.

Table 1 Circuit Parameters and Calculated R_SETN And M_RN For M_IN=¼

Using the conditions listed above for the N-channel MOSFET B, Figure 3 displays the results of a TINA-TI simulation of the circuit in Figure 1 implemented with R_SETN values calculated from the ideal case (5Ω under these conditions), the corrected case (Equation 1), and the average of these two.

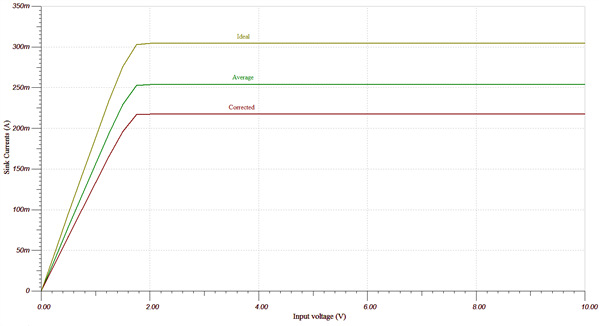Figure 3 Sink Current vs. Drain Voltage for Ideal, Corrected, and Average R_SETN Values

The results for simulations using both the N-channel MOSFET A and N-channel MOSFET B with the three R_SETN values (as described above) are summarized along with corresponding percent error calculations in Table 2 below.

Table 2 R_SETN Calculation Methods and Resulting Accuracy

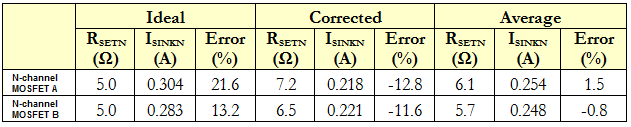
Ultimately a single feedback device can be used to derive a bias network of arbitrary values so long as certain conditions are met: particularly that the current in the primary feedback driven leg is the largest in the network, and the proper headroom is maintained in each leg. Thus, from a single voltage reference, a bias network is established.