米6体育平台手机版

ZHCADM0 January 2024 OPA2863 , OPA2863A

引言

有源滤波器可以减小电路板尺寸并降低成本，因此颇受欢迎，而且有源滤波器能够处理非常低的频率，这对于需要电感器的滤波器来说变得不切实际，因为电感器会变得非常大且成本高昂。在这些滤波器中，多反馈拓扑是一种常用的设计。有源滤波器的一个限制是超高频应用，这是由于放大器的带宽限制而导致的。许多免费的滤波器设计软件只是建议选择 GBWP 比滤波器带宽大 100 倍的器件，用于避免频率响应中的增益误差。对于更高带宽的滤波器，要找到符合标准的放大器可能很困难，有时甚至不可能做到。调整无源器件值则可以使频率响应明显更接近所需的滤波器形状。

理想放大器的 MFB 滤波器设计标准

图 1 中所示的 MFB 低通有源滤波器拓扑用于演示如何计算无源器件值以及非理想放大器对滤波器特性的影响。

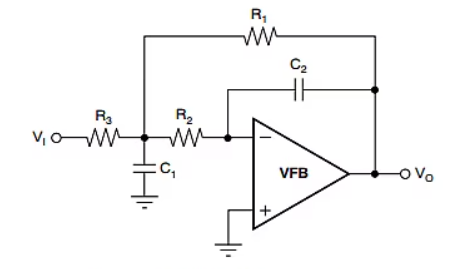图 1 MFB 滤波器拓扑

使用 MFB 有源滤波器拓扑时，需要确定五个无源器件值和三个滤波器特性。使用等效 R 设计方法方程式 1，可以找到 $R_{2}$ 的约束条件：

方程式 1.

R_{2} = \frac{- 2 k T}{{i_{n}}^{2}} (\frac{1 + A_{v}}{1 + 3 A v}) + \frac{1}{2} \sqrt{{(\frac{4 k T}{{i_{n}}^{2}})}^{2} {(\frac{1 + A_{v}}{1 + 3 A v})}^{2} + 4 {(\frac{e_{n}}{i_{n}})}^{2} (\frac{1 + A_{v}}{1 + 3 A v})}

该公式将返回 $R_{2}$ 的最大值，以便电阻噪声项等于放大器噪声电压。选择较低的 $R_{2}$ 值可以改善噪声。然而，选择 $R_{2}$ 时要慎重考虑，因为阻值太低会开始增加滤波器输出级和滤波器放大器输出级的负载。如果需要，可以将 $R_{2}$ 设置为更高值以减轻负载，但缺点是总输出噪声会更高。选择 $R_{2}$ 后，剩余的无源器件可使用以下公式计算：

方程式 2.

C_{2} = \frac{1}{ω_{0} R_{2} Q (2 A_{v} + 1)}

方程式 3.

C_{1} = \frac{Q}{ω_{0} R_{2} (1 - Q ω_{0} R_{2} C_{2} (1 + 4))}

方程式 4.

R_{3} = \frac{1}{A_{V} {ω_{0}}^{2} R_{2} C_{1} C_{2}}

方程式 5.

R_{1} = R_{3} A_{V}

其中 $A_{v}$ 表示滤波器所需的增益，Q 系数表示波特幅度图中的峰值，而 $ω_{o}$ 是滤波器的特性频率（以弧度为单位）。

非理想放大器的 MFB 滤波器传递函数

假设使用理想放大器，即没有其他极点影响滤波器的频率响应，则可得出 MFB 有源滤波器的上述特性。然而，主要设计障碍之一就是要考虑非理想放大器的影响。非理想放大器可以用单极模型来表示，其传递函数 A(s) 如下：

方程式 6.

A (s) = \frac{A_{o l} ω_{a}}{s + ω_{a}}

其中 A_ol 是直流时的放大器开环增益，ω_a 是主极点频率。可以使用方程式 7 计算出特定器件的 ω_a。

方程式 7.

ω_{a} = G B W P \times \frac{2 π}{A_{o l}} [r a d i a n s]

考虑到放大器的这个单极模型时，会向 MFB 滤波器的传递函数添加一个极点。然后，传递函数采用以下形式：

方程式 8.

H (s) = \frac{V_{o} (s)}{V_{i} (s)} = \frac{G}{s^{3} + B_{2} s^{2} + B_{1} s + B_{0}}

其中...

方程式 9.

G = \frac{A_{o l} ω_{a}}{C_{1} C_{2} R_{2} R_{3}}

方程式 10.

B_{2} = \frac{1}{R_{2} C_{2}} + \frac{1 + \frac{R_{1}}{R_{2} | | R_{3}}}{R_{2} C_{1}} + ω_{a} (1 + A_{o l})

方程式 11.

B_{1} = \frac{1 + \frac{R_{1}}{R_{3}}}{R_{1} R_{2} C_{1} C_{2}} + ω_{a} (\frac{1}{R_{2} C_{2}} + \frac{A_{o l} + 1}{R_{1} C_{1}} (1 + \frac{R_{1}}{R_{2} | | R_{3}}))

方程式 12.

B_{0} = \frac{ω_{a} (A_{o l} + 1 + \frac{R_{1}}{R_{3}})}{R_{1} R_{2} C_{1} C_{2}}

在此基础上，使用三次求解器确定复极对和实数解。复极解的形式为：

方程式 13.

P_{1、2} = a \pm j b

特性频率可由方程式 14 得出。

方程式 14.

ω_{o} ， a c t u a l = \sqrt{a^{2} + b^{2}} [r a d i a n s]

Q 系数可由方程式 15 得出。

方程式 15.

Q_{a c t u a l} = \frac{1}{2 c o s ({t a n}^{- 1} (\frac{b}{a}))}

调整非理想放大器的无源器件值

设计有源滤波器时，设计人员必须了解如何克服非理想放大器的局限性。如理想放大器的 MFB 滤波器设计标准所示，我们可以计算有源 MFB 滤波器的无源器件值，但频率响应取决于所选放大器的行为。使用非理想放大器的 MFB 滤波器传递函数中所示的公式，我们可以确定实际的滤波器行为，并使用这些行为来调整无源器件，以获得更接近所需滤波器形状的频率响应。

当选择 GBWP 比滤波器带宽大 100 倍的放大器不可行时，可以使用无源器件调整算法来降低频率响应中的增益误差，使频率响应明显更接近所需的滤波器形状。要调整无源器件值，一种方法是确定实际 Q 系数与所需 Q 系数之间的误差，以确定调整后的新 Q 系数，用于重新计算无源器件值。特性频率也必须遵循同样的过程。调整后的 Q 系数和调整后的特性频率可由以下公式得出：

方程式 16.

Q_{a d j u s t e d} = \frac{{Q_{t a r g e t}}^{2}}{Q_{a c t u a l}}

方程式 17.

ω_{o} ， a d j u s t e d = \frac{{ω_{o, t a r g e t}}^{2}}{ω_{o ， a c t u a l}}

将调整后的特性频率和 Q 系数值代入理想放大器的 MFB 滤波器设计标准中的目标特性频率和 Q 系数公式，可得出新的无源器件值，从而改善滤波器形状。

设计示例

为了说明带宽限制和无源器件调整对滤波器频率响应的影响，我们使用 OPA2863A 设计了一个二阶低通 MFB 滤波器。OPA2863A 具有 50MHz 的 GBWP。我们设计了三个具有不同特性频率的滤波器来显示带宽施加的限制。所有三个滤波器的目标 Q 系数均为 1，直流增益均为 2V/V。表 1 显示了设计低通 MFB 滤波器时不进行任何 RC 调整的结果。

表 1 不带 RC 校正功能的 MFB 滤波器

所需的截止频率	RI (Ω)	R2 (Ω)	R3 (Ω)	C1 (pF)	C2 (pF)	Q 系数	实际截止频率	误差百分比
500kHz	2000	1000	1000	1010	81	1.003	491.45kHz	1.71%
5MHz	2000	1000	1000	101	8.1	1.005	4.29MHz	14.2%
20MHz	2000	1000	1000	25.3	2.02	0.8953	12.38MHz	38.1%

然后，采用 RC 调整方法，通过考虑有限的放大器带宽来减小频率响应中的误差。表 2 中展示了相关结果。

表 2 带 RC 校正功能的 MFB 滤波器

所需的截止频率	RI (Ω)	R2 (Ω)	R3 (Ω)	C1 (pF)	C2 (pF)	Q 系数	实际截止频率	误差百分比
500kHz	2000	1000	1000	989	79.7	1.000	499.85kHz	0.03%
5MHz	2000	1000	1000	85	6.86	0.9961	4.95MHz	1.00%
20MHz	2000	1000	1000	17.3	1.11	0.8697	16.55MHz	17.25%

图 2、图 3 和图 4 显示了采用和不采用无源器件值校正方法时每种滤波器设计的频率响应。

图 2 500kHz 低通有源 MFB 滤波器

图 3 5MHz 低通有源 MFB 滤波器

图 4 20MHz 低通有源 MFB 滤波器

未考虑的因素

本文通篇的分析没有考虑到一些主题。首先，未考虑放大器反相输入引脚上的任何寄生电容。参考文献 4 更详细地介绍了该主题。另一个需要考虑但未在本应用简报中涉及的因素是不同器件的 GBWP 可能存在差异。根据温度和器件的不同，保守估计可能的 GBWP 变化约为 ±20% 至 ±30%，具体取决于放大器架构。本文中计算的无源器件值是理想值，并不总是标准电阻器值和电容器值。选择最接近理想值的标准器件值会产生一定的误差。此外，标准电阻器值和电容器值也会有变化，尽管变化较小（约 0.5% 至 1%），但如今更容易获得。

总结

设计有源滤波器时常见的问题之一是，实现所需滤波效果的最小 GBWP 应为多少。许多软件建议放大器的 GBWP 比滤波器带宽大 100 倍。然而，这会增加系统的额外成本，并且对功耗的要求更高。使用无源器件调整方法则可以将 GBWP 裕度从许多滤波器设计软件使用的 100 倍带宽显著降低。如设计示例所示，设计 GBWP 仅比滤波器带宽大 2.5 倍的有源滤波器时，与目标滤波器特性的误差约为 17%。由于需要较低的 GBWP 裕度，因此放大器的选择范围更广，甚至对于高频滤波器也是如此。

参考资料

米6体育平台手机版_好二三四 (TI)，ADC 接口应用中 MFB 滤波器的设计方法 应用报告。
Electronic Design News，Testing op amp tools for their active filter design accuracy and dynamic range 文章。
Planet Analog，Include the op amp gain bandwidth product in the Rauch low-pass active filter performance equations 文章。
Planet Analog，Use “true” gain-bandwidth product to estimate required margin in active filters, Insight #13 文章。
米6体育平台手机版_好二三四 (TI)，适合所有人的运算放大器 设计参考。
Pearson，SOLVING CUBIC EQUATIONS BY EXCEL 学术出版物。
米6体育平台手机版_好二三四 (TI)，OPAx863A 105MHz 轨到轨输入/输出高精度放大器 数据表。