ZHCU083I January   2013  – October 2021 TMS320F2802-Q1 , TMS320F28026-Q1 , TMS320F28026F , TMS320F28027-Q1 , TMS320F28027F , TMS320F28027F-Q1 , TMS320F28052-Q1 , TMS320F28052F , TMS320F28052F-Q1 , TMS320F28052M , TMS320F28052M-Q1 , TMS320F28054-Q1 , TMS320F28054F , TMS320F28054F-Q1 , TMS320F28054M , TMS320F28054M-Q1 , TMS320F2806-Q1 , TMS320F28062-Q1 , TMS320F28062F , TMS320F28062F-Q1 , TMS320F28068F , TMS320F28068M , TMS320F28069-Q1 , TMS320F28069F , TMS320F28069F-Q1 , TMS320F28069M , TMS320F28069M-Q1

 

  1.   Read This First
    1.     关于本手册
    2.     术语表
    3.     支持资源
    4.     商标
  2. 1 引言
    1. 1.1 InstaSPIN-FOC™ 和 FAST™ 概述
      1. 1.1.1 FAST™ 估算器特性
      2. 1.1.2 InstaSPIN-FOC™ 解决方案特性
      3. 1.1.3 InstaSPIN-FOC™ 方框图
      4. 1.1.4 将 FAST™ 估算器与典型解决方案相比较
      5. 1.1.5 FAST™ 提供无传感器 FOC 性能
        1. 1.1.5.1 FAST 估算器取代机械传感器
        2. 1.1.5.2 对性能十分关键的转子角准确度
    2. 1.2 InstaSPIN-MOTION™ 和 SpinTAC™ 概述
      1. 1.2.1 InstaSPIN-MOTION™ 关键功能和优势
        1. 1.2.1.1 FAST 统一软件观测器
        2. 1.2.1.2 SpinTAC 运动控制套件
          1. 1.2.1.2.1 IDENTIFY
          2. 1.2.1.2.2 CONTROL
          3. 1.2.1.2.3 MOVE
          4. 1.2.1.2.4 PLAN
        3. 1.2.1.3 其他 InstaSPIN-MOTION 特性
      2. 1.2.2 InstaSPIN-MOTION™ 方框图
      3. 1.2.3 应用示例
        1. 1.2.3.1 跑步机传送带：不同速度和负载下的平滑运动
        2. 1.2.3.2 摄像机：低速时的平滑运动和位置精度
        3. 1.2.3.3 洗衣机：低速时的平滑运动和位置准确度
          1. 1.2.3.3.1 搅动周期
          2. 1.2.3.3.2 旋转周期
          3. 1.2.3.3.3 InstaSPIN-MOTION 在整个工作范围内的运行
  3. 2 快速入门套件 - TI 提供的软件和硬件
    1. 2.1 概述
    2. 2.2 评估 InstaSPIN-FOC™ 和 InstaSPIN-MOTION™
  4. 3 InstaSPIN™ 和 MotorWare™
    1. 3.1 概述
    2. 3.2 MotorWare™ 目录结构
      1. 3.2.1 MotorWare™ – 驱动程序
      2. 3.2.2 MotorWare™ – ide
      3. 3.2.3 MotorWare™ – modules
      4. 3.2.4 MotorWare™ – solutions（解决方案）
    3. 3.3 MotorWare™ 面向对象的设计
      1. 3.3.1 对象
      2. 3.3.2 方法
        1. 3.3.2.1 Init 方法
        2. 3.3.2.2 Set 方法
        3. 3.3.2.3 Get 方法
        4. 3.3.2.4 Run 方法
    4. 3.4 InstaSPIN-FOC™ API
      1. 3.4.1 控制器 API 函数 - ctrl.c、ctrl.h、CTRL_obj.h
        1. 3.4.1.1 CTRL 枚举和结构
          1.        CTRL_Obj
          2.        CTRL_State_e
          3.        CTRL_ErrorCode_e
          4.        CTRL_TargetProc_e
          5.        CTRL_Type_e
          6.        CTRL_Version
        2. 3.4.1.2 CTRL 状态控制和错误处理
          1.        CTRL_initCtrl()
          2.        CTRL_updateState ()
          3.        CTRL_isError ()
          4.        CTRL_checkForErrors ()
        3. 3.4.1.3 CTRL Get 函数
          1.        CTRL_getCount_current ()
          2.        CTRL_getCount_isr ()
          3.        CTRL_getCount_speed ()
          4.        CTRL_getCount_state ()
          5.        CTRL_getCount_traj ()
          6.        CTRL_getCtrlFreq ()
          7.        CTRL_getCtrlPeriod_sec ()
          8.        CTRL_getErrorCode ()
          9.        CTRL_getEstHandle ()
          10.        CTRL_getFlag_enableCtrl ()
          11.        CTRL_getFlag_enableDcBusComp ()
          12.        CTRL_getFlag_enablePowerWarp ()
          13.        CTR CTRL_getFlag_enableOffset ()
          14.        CTRL_getFlag_enableSpeedCtrl ()
          15.        CTRL_getFlag_enableUserMotorParams ()
          16.        CTRL_getGains ()
          17.        CTRL_getIab_filt_pu ()
          18.        CTRL_getIab_filt_addr ()
          19.        CTRL_getIab_in_addr ()
          20.        CTRL_getIab_in_pu ()
          21.        CTRL_getId_in_pu ()
          22.        CTRL_getId_ref_pu ()
          23.        CTRL_getIdq_in_addr ()
          24.        CTRL_getIdq_in_pu ()
          25.        CTRL_getIdq_ref_pu ()
          26.        CTRL_getIdRated_pu ()
          27.        CTRL_getIq_in_pu ()
          28.        CTRL_getIq_ref_pu ()
          29.        CTRL_getKi ()
          30.        CTRL_getKd ()
          31.        CTRL_getKp ()
          32.        CTRL_getLhf ()
          33.        CTRL_getMagCurrent_pu ()
          34.        CTRL_getMaxVsMag_pu ()
          35.        CTRL_getMaximumSpeed_pu ()
          36.        CTRL_getMotorRatedFlux ()
          37.        CTRL_getMotorType ()
          38.        CTRL_getNumCtrlTicksPerCurrentTick ()
          39.        CTRL_getNumCtrlTicksPerSpeedTick ()
          40.        CTRL_getNumCtrlTicksPerTrajTick ()
          41.        CTRL_getNumIsrTicksPerCtrlTick ()
          42.        CTRL_getRefValue_pu ()
          43.        CTRL_getRhf ()
          44.        CTRL_getRoverL ()
          45.        CTRL_getSpd_max_pu ()
          46.        CTRL_getSpd_out_addr ()
          47.        CTRL_getSpd_out_pu ()
          48.        CTRL_getSpd_ref_pu ()
          49.        CTRL_getSpd_int_ref_pu ()
          50.        CTRL_getState ()
          51.        CTRL_getTrajFreq ()
          52.        CTRL_getTrajPeriod_sec ()
          53.        CTRL_getTrajStep ()
          54.        CTRL_getUi ()
          55.        CTRL_getVab_in_pu ()
          56.        CTRL_getVab_out_addr ()
          57.        CTRL_getVab_out_pu ()
          58.        CTRL_getVd_out_addr ()
          59.        CTRL_getVd_out_pu ()
          60.        CTRL_getVdq_out_addr ()
          61.        CTRL_getVdq_out_pu ()
          62.        CTRL_getVersion ()
          63.        CTRL_getVq_out_addr ()
          64.        CTRL_getVq_out_pu ()
          65.        CTRL_getWaitTime ()
        4. 3.4.1.4 CTRL 计数器函数
          1.        CTRL_incrCounter_current ()
          2.        CTRL_incrCounter_isr ()
          3.        CTRL_incrCounter_speed ()
          4.        CTRL_incrCounter_state ()
          5.        CTRL_incrCounter_traj ()
          6.        CTRL_resetCounter_current ()
          7.        CTRL_resetCounter_isr ()
          8.        CTRL_resetCounter_speed ()
          9.        CTRL_resetCounter_state ()
          10.        CTRL_resetCounter_traj ()
        5. 3.4.1.5 CTRL Set 函数
          1.        CTRL_setCtrlFreq_Hz ()
          2.        CTRL_setCtrlFreq_sec ()
          3.        CTRL_setErrorCode ()
          4.        CTRL_setEstParams ()
          5.        CTRL_setFlag_enableCtrl ()
          6.        CTRL_setFlag_enableDcBusComp ()
          7.        CTRL_setFlag_enablePowerWarp ()
          8.        CTRL_setFlag_enableOffset ()
          9.        calibrationCTRL_setFlag_enableSpeedCtrl ()
          10.        CTRL_setFlag_enableUserMotorParams ()
          11.        CTRL_setGains ()
          12.        CTRL_setIab_in_pu ()
          13.        CTRL_setIab_filt_pu ()
          14.        CTRL_setId_ref_pu ()
          15.        CTRL_setIdq_in_pu ()
          16.        CTRL_setIdq_ref_pu ()
          17.        CTRL_setIdRated_pu ()
          18.        CTRL_setIq_ref_pu ()
          19.        CTRL_setKd ()
          20.        CTRL_setKi ()
          21.        CTRL_setKp ()
          22.        CTRL_setLhf ()
          23.        CTRL_setMagCurrent_pu ()
          24.        CTRL_setMaxVsMag_pu ()
          25.        CTRL_setMaxAccel_pu ()
          26.        CTRL_setMaximumSpeed_pu ()
          27.        CTRL_setParams()
          28.        CTRL_setNumCtrlTicksPerCurrentTick ()
          29.        CTRL_setNumCtrlTicksPerSpeedTick ()
          30.        CTRL_setNumCtrlTicksPerTrajTick ()
          31.        CTRL_setNumIsrTicksPerCtrlTick ()
          32.        CTRL_setRhf ()
          33.        CTRL_setRoverL ()
          34.        CTRL_setSpdMax ()
          35.        CTRL_setSpd_max_pu ()
          36.        CTRL_setSpd_out_pu ()
          37.        CTRL_setSpd_ref_pu ()
          38.        CTRL_setSpd_ref_krpm ()
          39.        CTRL_setState ()
          40.        CTRL_setTrajFreq_Hz ()
          41.        CTRL_setTrajPeriod_sec ()
          42.        CTRL_setUi ()
          43.        CTRL_setupClarke_I ()
          44.        CTRL_setupClarke_V ()
          45.        CTRL_setupEstIdleState ()
          46.        CTRL_setupEstOnLineState ()
          47.        CTRL_setUserMotorParams ()
          48.        CTRL_setVab_in_pu ()
          49.        CTRL_setVab_out_pu ()
          50.        CTRL_setVdq_out_pu ()
          51.        CTRL_setWaitTimes ()
          52.        CTRL_setup ()
          53.        CTRL_setupCtrl ()
          54.        CTRL_setupEst ()
          55.        CTRL_setupTraj ()
        6. 3.4.1.6 CTRL Run 和 Compute 函数
          1.        CTRL_angleDelayComp ()
          2.        CTRL_computePhasor ()
          3.        CTRL_doCurrentCtrl ()
          4.        CTRL_doSpeedCtrl ()
          5.        CTRL_run()
          6.        CTRL_runTraj ()
          7.        CTRL_runOffLine ()
          8.        CTRL_runOnLine ()
          9.        CTRL_runOnLine_User ()
          10.        CTRL_useZeroIq_ref ()
      2. 3.4.2 估算器 API 函数 - FAST™ 库 - est.h、est_states.h
        1. 3.4.2.1 EST 枚举和结构
          1.        EST_RsOnLineFilterType_e
          2.        EST_ErrorCode_e
          3.        EST_State_e
        2. 3.4.2.2 EST Set 函数
          1.        EST_setRsOnLineId_pu ()
          2.        EST_setAngle_pu ()
          3.        EST_setDcBus_pu ()
          4.        EST_setDir_qFmt ()
          5.        EST_setFe_neg_max_pu ()
          6.        EST_setFe_pos_min_pu ()
          7.        EST_setFlag_enableFluxControl ()
          8.        EST_setFlag_enableForceAngle ()
          9.        EST_setFlag_enableRsOnLine ()
          10.        EST_setFlag_enableRsRecalc ()
          11.        EST_setFlag_estComplete ()
          12.        EST_setFlag_updateRs ()
          13.        EST_setForceAngleDelta_pu ()
          14.        EST_setFreqB0_lp_pu ()
          15.        EST_setFreqBeta_lp_pu ()
          16.        EST_setFullScaleCurrent ()
          17.        EST_setFullScaleFlux ()
          18.        EST_setFullScaleFreq ()
          19.        EST_setFullScaleInductance ()
          20.        EST_setFullScaleResistance ()
          21.        EST_setFullScaleVoltage ()
          22.        EST_setIdle ()
          23.        EST_setIdle_all ()
          24.        EST_setId_ref_pu ()
          25.        EST_setIdRated_pu ()
          26.        EST_setIq_ref_pu ()
          27.        EST_setLs_d_pu ()
          28.        EST_setLs_delta_pu ()
          29.        EST_setLs_dq_pu ()
          30.        EST_setLs_q_pu ()
          31.        EST_setLs_qFmt ()
          32.        EST_setMaxAccel_pu ()
          33.        EST_setMaxAccel_est_pu ()
          34.        EST_setMaxCurrentSlope_pu ()
          35.        EST_setMaxCurrentSlope_PowerWarp_pu ()
          36.        EST_setRr_pu ()
          37.        EST_setRr_qFmt ()
          38.        EST_setRs_delta_pu ()
          39.        EST_setRsOnLine_pu ()
          40.        EST_setRsOnLine_qFmt ()
          41.        EST_setRsOnLineFilterParams ()
          42.        EST_setRsOnLineId_mag_pu ()
          43.        EST_setRs_pu ()
          44.        EST_setRs_qFmt ()
          45.        EST_updateId_ref_pu ()
        3. 3.4.2.3 EST Get 函数
          1.        EST_get_krpm_to_pu_sf ()
          2.        EST_get_pu_to_krpm_sf ()
          3.        EST_getAngle_pu ()
          4.        EST_getDcBus_pu ()
          5.        EST_ErrorCode_e EST_getErrorCode ()
          6.        EST_getFe ()
          7.        EST_getFe_pu ()
          8.        EST_getFlag_enableForceAngle ()
          9.        EST_getFlag_enableRsOnLine ()
          10.        EST_getFlag_enableRsRecalc ()
          11.        EST_getFlag_estComplete ()
          12.        EST_getFlag_updateRs ()
          13.        EST_getFlux_VpHz ()
          14.        EST_getFlux_Wb ()
          15.        EST_getFlux_pu ()
          16.        EST_getFm ()
          17.        EST_getFm_pu ()
          18.        EST_getForceAngleDelta_pu ()
          19.        EST_getForceAngleStatus ()
          20.        EST_getFreqB0_lp_pu ()
          21.        EST_getFreqBeta_lp_pu ()
          22.        EST_getFslip ()
          23.        281
          24.        EST_getFslip_pu ()
          25.        EST_getFullScaleCurrent ()
          26.        EST_getFullScaleFlux ()
          27.        EST_getFullScaleFreq ()
          28.        EST_getFullScaleInductance ()
          29.        EST_getFullScaleResistance ()
          30.        EST_getFullScaleVoltage ()
          31.        EST_getIdRated ()
          32.        EST_getIdRated_pu ()
          33.        EST_getIdRated_indEst_pu ()
          34.        EST_getIdRated_ratedFlux_pu ()
          35.        EST_getLr_H ()
          36.        EST_getLr_pu ()
          37.        EST_getLr_qFmt ()
          38.        EST_getLs_d_H ()
          39.        EST_getLs_d_pu ()
          40.        EST_getLs_delta_pu ()
          41.        EST_getLs_dq_pu ()
          42.        EST_getLs_q_H ()
          43.        EST_getLs_q_pu ()
          44.        EST_getLs_qFmt ()
          45.        EST_getLs_max_pu ()
          46.        EST_getLs_min_pu ()
          47.        EST_getLs_coarse_max_pu ()
          48.        EST_getMaxAccel_pu ()
          49.        EST_getMaxAccel_est_pu ()
          50.        EST_getMaxCurrentSlope_pu ()
          51.        EST_getMaxCurrentSlope_PowerWarp_pu ()
          52.        EST_getOneOverDcBus_pu ()
          53.        EST_getRr_Ohm ()
          54.        EST_getRr_pu ()
          55.        EST_getRr_qFmt ()
          56.        EST_getRs_delta_pu ()
          57.        EST_getRs_Ohm ()
          58.        EST_getRs_pu ()
          59.        EST_getRs_qFmt ()
          60.        EST_getRs_qFmt ()
          61.        EST_getRsOnLine_Ohm ()
          62.        EST_getRsOnLine_pu ()
          63.        EST_getRsOnLineId_mag_pu ()
          64.        EST_getRsOnLineId_pu ()
          65.        EST_getSpeed_krpm ()
          66.        EST_getSignOfDirection ()
          67.        EST_getSpeed_krpm ()
          68.        EST_getState ()
          69.        EST_getTorque_lbin ()
          70.        EST_getTorque_Nm ()
          71.        EST_getDir_qFmt ()
        4. 3.4.2.4 EST Run 和 Compute 函数
          1.        EST_computeLr_H ()
          2.        EST_doCurrentCtrl ()
          3.        EST_genOutputLimits_Pid_Id ()
          4.        EST_genOutputLimits_Pid_Iq ()
          5.        EST_run ()
          6.        EST_computeDirection_qFmt ()
        5. 3.4.2.5 EST 计数器函数
          1.        EST_resetCounter_ctrl ()
          2.        EST_resetCounter_state ()
        6. 3.4.2.6 EST 状态控制和错误处理函数
          1.        EST_isError ()
          2.        EST_isIdle ()
          3.        EST_isLockRotor ()
          4.        EST_isMotorIdentified ()
          5.        EST_isOnLine ()
          6.        EST_updateState ()
          7.        EST_useZeroIq_ref ()
      3. 3.4.3 硬件抽象层 (HAL) API 函数 - hal.c、hal.h、hal_obj.h
        1. 3.4.3.1 HAL 枚举和结构
          1.        HAL_AdcData_t
          2.        HAL_DacData_t
          3.        HAL_PwmData_t
          4.        HAL_LedNumber_e
          5.        GPIO_Number_e
          6.        HAL_SensorType_e
          7.        HAL_Obj
        2. 3.4.3.2 HAL – ADC 和 AFE
          1.        HAL_setupAdcs ()
          2.        HAL_setupAfe ()
          3.        HAL_acqAdcInt ()
          4.        HAL_readAdcData()
          5.        HAL_updateAdcBias ()
          6.        HAL_setBias ()
          7.        HAL_getBias ()
          8.        HAL_cal ()
          9.        HAL_AdcCalConversion ()
          10.        HAL_AdcOffsetSelfCal ()
          11.        HAL_getAdcSocSampleDelay ()
          12.        HAL_setAdcSocSampleDelay ()
          13.        HAL_getCurrentScaleFactor ()
          14.        HAL_setCurrentScaleFactor ()
          15.        HAL_getVoltageScaleFactor ()
          16.        HAL_setVoltageScaleFactor ()
          17.        HAL_getNumCurrentSensors ()
          18.        HAL_setNumCurrentSensors ()
          19.        HAL_getNumVoltageSensors ()
          20.        HAL_setNumVoltageSensors ()
          21.        378
          22.        HAL_getOffsetBeta_lp_pu ()
          23.        HAL_setOffsetBeta_lp_pu ()
          24.        HAL_setOffsetInitCond ()
          25.        HAL_getOffsetValue ()
          26.        HAL_setOffsetValue ()
          27.        HAL_runOffsetEst ()
        3. 3.4.3.3 HAL – PWM 和 PWM-DAC
          1.        HAL_setupPwms ()
          2.        HAL_setupPwmDacs ()
          3.        HAL_readTimerCnt ()
          4.        HAL_reloadTimer ()
          5.        HAL_readPwmPeriod ()
          6.        HAL_disablePwm ()
          7.        HAL_enablePwm ()
          8.        HAL_writeDacData ()
          9.        HAL_writePwmData()
          10.        HAL_readPwmCmpA ()
          11.        HAL_readPwmCmpB ()
          12.        HAL_setTrigger ()
          13.        HAL_acqPwmInt ()
          14.        HAL_enablePwmInt ()
          15.        HAL_hvProtection ()
        4. 3.4.3.4 HAL – CPU 定时器
          1.        HAL_setupClks ()
          2.        HAL_setupTimers ()
          3.        HAL_startTimer ()
          4.        HAL_stopTimer ()
          5.        HAL_setTimerPeriod ()
          6.        HAL_getTimerPeriod ()
        5. 3.4.3.5 HAL – GPIO 和 LED
          1.        HAL_setupGpios ()
          2.        HAL_toggleGpio ()
          3.        HAL_setGpioHigh ()
          4.        HAL_setGpioLow ()
          5.        HAL_toggleLed
        6. 3.4.3.6 HAL – 其他
          1.        HAL_init()
          2.        HAL_initIntVectorTable ()
          3.        HAL_setParams ()
          4.        HAL_setupFlash ()
          5.        HAL_setupPie ()
          6.        HAL_setupPll ()
          7.        HAL_setupPeripheralClks ()
          8.        HAL_getOscTrimValue ()
          9.        HAL_OscTempComp ()
          10.        HAL_osc1Comp ()
          11.        HAL_osc2Comp ()
          12.        HAL_setupFaults ()
          13.        HAL_setParams ()
          14.        HAL_enableDebugInt ()
          15.        HAL_enableGlobalInts ()
          16.        HAL_disableGlobalInts ()
          17.        HAL_disableWdog ()
      4. 3.4.4 用户设置 – user.c、user.h、userParams.h
        1. 3.4.4.1 USER 枚举和结构
          1.        Struct_USER_Params_
          2.        USER_ErrorCode_e
        2. 3.4.4.2 USER Set 和 Compute 函数
          1.        USER_setParams()
          2.        USER_calcPIgains ()
          3.        USER_computeTorque_Ls_Id_Iq_pu_to_Nm_sf ()
          4.        USER_computeTorque_Flux_Iq_pu_to_Nm_sf ()
          5.        USER_computeFlux_pu_to_Wb_sf ()
          6.        USER_computeFlux_pu_to_VpHz_sf ()
          7.        USER_computeFlux ()
          8.        USER_computeTorque_Nm ()
          9.        USER_computeTorque_lbin ()
        3. 3.4.4.3 USER 错误处理函数
          1.        USER_checkForErrors ()
          2.        USER_getErrorCode ()
          3.        USER_setErrorCode ()
      5. 3.4.5 其他函数
        1.       softwareUpdate1p6 ()
    5. 3.5 InstaSPIN-MOTION™ 和 SpinTAC™ API
      1. 3.5.1 头文件、公共库和 ROM 库
      2. 3.5.2 版本信息
        1. 3.5.2.1 返回 SpinTAC™ 版本信息的代码示例
          1. 3.5.2.1.1 包括头文件
          2. 3.5.2.1.2 声明全局结构
          3. 3.5.2.1.3 初始化配置变量
          4. 3.5.2.1.4 返回版本信息
      3. 3.5.3 SpinTAC 结构名称
      4. 3.5.4 SpinTAC™ 变量
    6. 3.6 SpinTAC™ API
      1. 3.6.1 SpinTAC™ 速度控制
        1. 3.6.1.1 SpinTAC™ 速度控制接口
        2. 3.6.1.2 SpinTAC™ 速度控制运行函数
      2. 3.6.2 SpinTAC™ 速度移动
        1. 3.6.2.1 SpinTAC™ 速度移动接口
        2. 3.6.2.2 SpinTAC™ 速度移动运行函数
      3. 3.6.3 SpinTAC™ 速度规划
        1. 3.6.3.1 SpinTAC™ 速度规划接口
        2. 3.6.3.2 SpinTAC™ 速度规划主函数
      4. 3.6.4 SpinTAC™ 速度识别
        1. 3.6.4.1 SpinTAC™ 速度识别接口
        2. 3.6.4.2 SpinTAC™ 速度识别运行函数
      5. 3.6.5 SpinTAC™ 位置转换
        1. 3.6.5.1 SpinTAC™ 位置转换接口
        2. 3.6.5.2 SpinTAC™ 位置转换运行函数
      6. 3.6.6 SpinTAC™ 位置控制
        1. 3.6.6.1 SpinTAC™ 位置控制接口
        2. 3.6.6.2 SpinTAC™ 位置控制运行函数
      7. 3.6.7 SpinTAC™ 位置移动
        1. 3.6.7.1 SpinTAC™ 位置移动接口
        2. 3.6.7.2 SpinTAC™ 位置移动运行函数
      8. 3.6.8 SpinTAC™ 位置规划
        1. 3.6.8.1 SpinTAC™ 位置规划接口
        2. 3.6.8.2 SpinTAC 位置规划主函数
      9. 3.6.9 SpinTAC™ 函数
  5. 4 用户参数 (user.h)
    1. 4.1 电流和电压
      1. 4.1.1  USER_IQ_FULL_SCALE_FREQ_Hz
      2. 4.1.2  USER_IQ_FULL_SCALE_VOLTAGE_V
      3. 4.1.3  USER_ADC_FULL_SCALE_VOLTAGE_V
      4. 4.1.4  USER_VOLTAGE_SF
      5. 4.1.5  USER_IQ_FULL_SCALE_CURRENT_A
      6. 4.1.6  USER_ADC_FULL_SCALE_CURRENT_A
      7. 4.1.7  USER_CURRENT_SF
      8. 4.1.8  USER_NUM_CURRENT_SENSORS
      9. 4.1.9  USER_NUM_VOLTAGE_SENSORS
      10. 4.1.10 I_A_offset、I_B_offset、I_C_offset
      11. 4.1.11 V_A_offset、V_B_offset、V_C_offset
    2. 4.2 时钟与定时器
      1. 4.2.1 USER_SYSTEM_FREQ_MHz
      2. 4.2.2 USER_PWM_FREQ_kHz
      3. 4.2.3 USER_MAX_VS_MAG_PU
      4. 4.2.4 USER_PWM_PERIOD_usec
      5. 4.2.5 USER_ISR_FREQ_Hz
      6. 4.2.6 USER_ISR_PERIOD_usec
    3. 4.3 抽取率
      1. 4.3.1  USER_NUM_PWM_TICKS_PER_ISR_TICK
      2. 4.3.2  USER_NUM_ISR_TICKS_PER_CTRL_TICK
      3. 4.3.3  USER_NUM_CTRL_TICKS_PER_CURRENT_TICK
      4. 4.3.4  USER_NUM_CTRL_TICKS_PER_EST_TICK
      5. 4.3.5  USER_NUM_CTRL_TICKS_PER_SPEED_TICK
      6. 4.3.6  USER_NUM_CTRL_TICKS_PER_TRAJ_TICK
      7. 4.3.7  USER_CTRL_FREQ_Hz
      8. 4.3.8  USER_EST_FREQ_Hz
      9. 4.3.9  USER_TRAJ_FREQ_Hz
      10. 4.3.10 USER_CTRL_PERIOD_usec
      11. 4.3.11 USER_CTRL_PERIOD_sec
    4. 4.4 限制
      1. 4.4.1  USER_MAX_NEGATIVE_ID_REF_CURRENT_A
      2. 4.4.2  USER_ZEROSPEEDLIMIT
      3. 4.4.3  USER_FORCE_ANGLE_FREQ_Hz
      4. 4.4.4  USER_MAX_CURRENT_SLOPE_POWERWARP
      5. 4.4.5  USER_MAX_ACCEL_Hzps
      6. 4.4.6  USER_MAX_ACCEL_EST_Hzps
      7. 4.4.7  USER_MAX_CURRENT_SLOPE
      8. 4.4.8  USER_IDRATED_FRACTION_FOR_RATED_FLUX
      9. 4.4.9  USER_IDRATED_FRACTION_FOR_L_IDENT
      10. 4.4.10 USER_IDRATED_DELTA
      11. 4.4.11 USER_SPEEDMAX_FRACTION_FOR_L_IDENT
      12. 4.4.12 USER_FLUX_FRACTION
      13. 4.4.13 USER_POWERWARP_GAIN
      14. 4.4.14 USER_R_OVER_L_EST_FREQ_Hz
    5. 4.5 极
      1. 4.5.1 USER_VOLTAGE_FILTER_POLE_Hz
      2. 4.5.2 USER_VOLTAGE_FILTER_POLE_rps
      3. 4.5.3 USER_OFFSET_POLE_rps
      4. 4.5.4 USER_FLUX_POLE_rps
      5. 4.5.5 USER_DIRECTION_POLE_rps
      6. 4.5.6 USER_SPEED_POLE_rps
      7. 4.5.7 USER_DCBUS_POLE_rps
      8. 4.5.8 USER_EST_KAPPAQ
    6. 4.6 使用电机和识别设置
      1. 4.6.1  USER_MOTOR_TYPE
      2. 4.6.2  USER_MOTOR_NUM_POLE_PAIRS
      3. 4.6.3  USER_MOTOR_Rr
      4. 4.6.4  USER_MOTOR_Rs
      5. 4.6.5  USER_MOTOR_Ls_d
      6. 4.6.6  USER_MOTOR_Ls_q
      7. 4.6.7  USER_MOTOR_RATED_FLUX
      8. 4.6.8  USER_MOTOR_MAGNETIZING_CURRENT
      9. 4.6.9  USER_MOTOR_RES_EST_CURRENT
      10. 4.6.10 USER_MOTOR_IND_EST_CURRENT
      11. 4.6.11 USER_MOTOR_MAX_CURRENT
      12. 4.6.12 USER_MOTOR_FLUX_EST_FREQ_Hz
      13. 4.6.13 USER_MOTOR_ENCODER_LINES（仅限 InstaSPIN-MOTION™）
      14. 4.6.14 USER_MOTOR_MAX_SPEED_KRPM（仅限 InstaSPIN-MOTION™）
      15. 4.6.15 USER_SYSTEM_INERTIA（仅限 InstaSPIN-MOTION™）
      16. 4.6.16 USER_SYSTEM_FRICTION（仅限 InstaSPIN-MOTION）
      17. 4.6.17 USER_SYSTEM_BANDWIDTH_SCALE（仅限 InstaSPIN-MOTION™）
    7. 4.7 SpinTAC™ 参数（spintac_velocity.h 和 spintac_position.h）
      1. 4.7.1 宏定义
        1. 4.7.1.1  ST_MREV_ROLLOVER（仅限 spintac_position.h）
        2. 4.7.1.2  ST_EREV_MAXIMUM（仅限 spintac_position.h）
        3. 4.7.1.3  ST_POS_ERROR_MAXIMUM_MREV（仅限 spintac_position.h）
        4. 4.7.1.4  ST_ISR_TICKS_PER_SPINTAC_TICK
        5. 4.7.1.5  ST_SPEED_SAMPLE_TIME
        6. 4.7.1.6  ST_SPEED_PU_PER_KRPM
        7. 4.7.1.7  ST_SPEED_KRPM_PER_PU
        8. 4.7.1.8  ST_MOTOR_INERTIA_PU
        9. 4.7.1.9  ST_MOTOR_FRICTION_PU
        10. 4.7.1.10 ST_MIN_ID_SPEED_RPM
        11. 4.7.1.11 ST_MIN_ID_SPEED_PU
        12. 4.7.1.12 ST_ID_INCOMPLETE_ERROR
        13. 4.7.1.13 ST_VARS_DEFAULTS
      2. 4.7.2 类型定义
        1. 4.7.2.1 VEL_Params_t/POS_Params_t
        2. 4.7.2.2 ST_Obj
        3. 4.7.2.3 ST_Handle
        4. 4.7.2.4 ST_PlanButton_e
        5. 4.7.2.5 ST_Vars_t
      3. 4.7.3 函数
        1. 4.7.3.1  ST_init
        2. 4.7.3.2  ST_setupPosConv
        3. 4.7.3.3  ST_setupVelCtl（仅限速度控制）
        4. 4.7.3.4  ST_setupPosCtl（仅限位置控制）
        5. 4.7.3.5  ST_setupVelMove（仅限速度控制）
        6. 4.7.3.6  ST_setupPosMove（仅限位置控制）
        7. 4.7.3.7  ST_setupVelPlan（仅限速度控制）
        8. 4.7.3.8  ST_setupPosPlan（仅限位置控制）
        9. 4.7.3.9  ST_setupVelId（仅限速度控制）
        10. 4.7.3.10 ST_runPosConv
        11. 4.7.3.11 ST_runVelCtl（仅限速度控制）
        12. 4.7.3.12 ST_runPosCtl（仅限位置控制）
        13. 4.7.3.13 ST_runVelMove（仅限速度控制）
        14. 4.7.3.14 ST_runPosMove（仅限位置控制）
        15. 4.7.3.15 ST_runVelPlan（仅限速度控制）
        16. 4.7.3.16 ST_runVelPlanTick（仅限速度控制）
        17. 4.7.3.17 ST_runPosPlan（仅限位置控制）
        18. 4.7.3.18 ST_runPosPlanTick（仅限位置控制）
        19. 4.7.3.19 ST_runVelId（仅限速度控制）
    8. 4.8 在 user.h 中设置 ACIM 电机参数
      1. 4.8.1 从 ACIM 数据表中获取这些参数
        1. 4.8.1.1 极对数
        2. 4.8.1.2 将数据表中的 ACIM 电机参数输入 user.h 中
        3. 4.8.1.3 获取 ACIM 的额定磁化电流
        4. 4.8.1.4 获取 ACIM 的额定磁通
  6. 5 管理电机信号
    1. 5.1 软件必要条件
      1. 5.1.1 IQ 满量程频率
      2. 5.1.2 IQ 满量程电压
      3. 5.1.3 IQ 满量程电流
      4. 5.1.4 最大电流
      5. 5.1.5 抽取率
      6. 5.1.6 系统频率
      7. 5.1.7 PWM 频率
      8. 5.1.8 最大电压矢量
    2. 5.2 硬件必要条件
      1. 5.2.1 电流反馈增益
      2. 5.2.2 电流反馈极性
        1. 5.2.2.1 正反馈
        2. 5.2.2.2 负反馈
      3. 5.2.3 电压反馈
      4. 5.2.4 电压滤波器极点
      5. 5.2.5 分流电阻器数量
      6. 5.2.6 死区时间配置
      7. 5.2.7 模拟输入配置
      8. 5.2.8 PWM 输出配置
  7. 6 电机识别和状态图
    1. 6.1  概述
    2. 6.2  InstaSPIN™ 电机识别
    3. 6.3  电机识别过程概述
      1. 6.3.1 控制器 (CTRL) 状态机
      2. 6.3.2 估算器 (EST) 状态机
      3. 6.3.3 控制器 (CTRL) 和估算器 (EST) 状态机的相关性
    4. 6.4  PMSM 和 ACIM 识别过程的差别
    5. 6.5  必要条件
      1. 6.5.1 机械必要条件
        1. 6.5.1.1 电机连接
        2. 6.5.1.2 相序
        3. 6.5.1.3 最小机械负载
      2. 6.5.2 硬件必要条件
      3. 6.5.3 软件必要条件
      4. 6.5.4 PMSM 电机识别的软件配置
        1. 6.5.4.1 电机类型
        2. 6.5.4.2 极对数
        3. 6.5.4.3 Rhf 和 Lhf 频率
        4. 6.5.4.4 Rs 电流
        5. 6.5.4.5 Ls 电流
        6. 6.5.4.6 Ls 和磁通频率
      5. 6.5.5 ACIM 电机识别的软件配置
        1. 6.5.5.1 电机类型
        2. 6.5.5.2 极对数
        3. 6.5.5.3 Rhf 和 Lhf 频率
        4. 6.5.5.4 额定磁通
        5. 6.5.5.5 Rs 电流
        6. 6.5.5.6 IdRated、Ls 和 Rr 频率
    6. 6.6  PMSM 电机完全识别
      1. 6.6.1  CTRL_State_Idle 和 EST_State_Idle
      2. 6.6.2  CTRL_State_OffLine 和 EST_State_Idle（硬件偏移已校准）
      3. 6.6.3  CTRL_State_OnLine 和 EST_State_RoverL
        1. 6.6.3.1 RoverL 状态下注入电流的幅值
        2. 6.6.3.2 RoverL 状态下注入电流的频率
        3. 6.6.3.3 RoverL 状态下的测量时间
        4. 6.6.3.4 RoverL 识别期间的电流控制器稳定性故障排除
        5. 6.6.3.5 调节高速电机产生的电流控制器增益
      4. 6.6.4  CTRL_State_OnLine 和 EST_State_Rs
        1. 6.6.4.1 Rs 识别期间的电流控制器稳定性故障排除
      5. 6.6.5  CTRL_State_OnLine 和 EST_State_RampUp
        1. 6.6.5.1 斜升电流幅值
          1. 6.6.5.1.1 斜升期间的电机转轴停转故障排除
        2. 6.6.5.2 斜升时间和加速度
          1. 6.6.5.2.1 平滑斜坡的电机转轴故障排除
        3. 6.6.5.3 PMSM 最终斜升速度
      6. 6.6.6  CTRL_State_OnLine 和 EST_State_RatedFlux
        1. 6.6.6.1 电流斜降
        2. 6.6.6.2 总测量时间
        3. 6.6.6.3 磁通测量故障排除
      7. 6.6.7  CTRL_State_OnLine 和 EST_State_Ls
        1. 6.6.7.1 斜升电流
        2. 6.6.7.2 Ls 识别故障排除
        3. 6.6.7.3 Ls_d 和 Ls_q（定子直流电感和定子正交电感）
      8. 6.6.8  CTRL_State_OnLine 和 EST_State_RampDown
      9. 6.6.9  CTRL_State_OnLine 和 EST_State_MotorIdentified
      10. 6.6.10 CTRL_State_Idle 和 EST_State_Idle
    7. 6.7  ACIM 电机完全识别
      1. 6.7.1  CTRL_State_Idle 和 EST_State_Idle
      2. 6.7.2  CTRL_State_OffLine 和 EST_State_Idle
      3. 6.7.3  CTRL_State_OnLine 和 EST_State_RoverL
      4. 6.7.4  CTRL_State_OnLine 和 EST_State_Rs
      5. 6.7.5  CTRL_State_OnLine 和 EST_State_RampUp
        1. 6.7.5.1 ACIM 最终斜升速度
      6. 6.7.6  CTRL_State_OnLine 和 EST_State_IdRated
        1. 6.7.6.1 减少振荡以改善 Id 额定电流测量
        2. 6.7.6.2 读取 Id 额定电流最终值
      7. 6.7.7  CTRL_State_OnLine 和 EST_State_RatedFlux
        1. 6.7.7.1 磁通测量故障排除
      8. 6.7.8  CTRL_State_OnLine 和 EST_State_RampDown
      9. 6.7.9  CTRL_State_Idle 和 EST_State_LockRotor
        1. 6.7.9.1 锁定转子测试故障排除
      10. 6.7.10 CTRL_State_OnLine 和 EST_State_Ls
      11. 6.7.11 CTRL_State_OnLine 和 EST_State_Rr
      12. 6.7.12 CTRL_State_OnLine 和 EST_State_RampDown
      13. 6.7.13 CTRL_State_OnLine 和 EST_State_MotorIdentified
      14. 6.7.14 CTRL_State_Idle 和 EST_State_Idle
    8. 6.8  PMSM 和 ACIM 电机识别重校准
      1. 6.8.1 完全识别后的 PMSM 和 ACIM 电机重校准
        1. 6.8.1.1 启动阶段注意事项
        2. 6.8.1.2 CTRL_State_Idle 和 EST_State_Idle
        3. 6.8.1.3 CTRL_State_OffLine 和 EST_State_Idle
        4. 6.8.1.4 CTRL_State_OnLine 和 EST_State_Rs
          1. 6.8.1.4.1 管理 Rs 重校准所需的时间
          2. 6.8.1.4.2 Rs 重校准的软件配置
        5. 6.8.1.5 CTRL_State_OnLine 和 EST_State_OnLine
          1. 6.8.1.5.1 从 CTRL 在线状态和 EST Rs 状态转换到在线状态
          2. 6.8.1.5.2 从（CTRL 空闲状态或 CTRL 离线状态）和 EST 空闲状态转换到在线状态
        6. 6.8.1.6 CTRL_State_Idle 和 EST_State_Idle
      2. 6.8.2 使用 user.h 中的参数后的 PMSM 和 ACIM 电机重校准
    9. 6.9  在 user.h 中设置 PMSM 电机参数
      1. 6.9.1 从 PMSM 数据表中获取参数
        1. 6.9.1.1 极对数
        2. 6.9.1.2 定子电阻 (Rs)
        3. 6.9.1.3 定子电感（Ls_d 和 Ls_q）
        4. 6.9.1.4 额定磁通 (ψ)
    10. 6.10 电机识别故障排除
      1. 6.10.1 PMSM 电机识别故障排除
        1. 6.10.1.1 在负载无法断开时识别 PMSM 电机
        2. 6.10.1.2 电机能否在连接负载的情况下旋转？
        3. 6.10.1.3 运行电机识别的前三个步骤
        4. 6.10.1.4 通过 user.h 中的电机参数运行
        5. 6.10.1.5 斜升期间的电机转轴停转故障排除
        6. 6.10.1.6 平滑斜坡的电机转轴故障排除
        7. 6.10.1.7 磁通测量故障排除
        8. 6.10.1.8 Ls 识别故障排除
          1. 6.10.1.8.1 识别低电感 PMSM 电机
            1. 6.10.1.8.1.1 硬件注意事项
            2. 6.10.1.8.1.2 软件注意事项
          2. 6.10.1.8.2 识别凸极 PMSM 电机的电感
            1. 6.10.1.8.2.1 硬件注意事项
            2. 6.10.1.8.2.2 软件注意事项
        9. 6.10.1.9 识别高齿槽转矩 PMSM 电机
      2. 6.10.2 ACIM 电机识别故障排除
        1. 6.10.2.1 磁通测量故障排除
        2. 6.10.2.2 锁定转子测试故障排除
  8. 7 惯性识别
    1. 7.1 概述
    2. 7.2 InstaSPIN-MOTION™ 惯性识别
    3. 7.3 惯性识别过程概述
    4. 7.4 SpinTAC™ 速度识别的软件配置
      1. 7.4.1 包括头文件
      2. 7.4.2 声明全局变量
      3. 7.4.3 初始化配置变量
      4. 7.4.4 调用 SpinTAC™ 速度识别
    5. 7.5 惯性识别故障排除
      1. 7.5.1 ERR_ID
      2. 7.5.2 2003 错误
      3. 7.5.3 2004 错误
        1. 7.5.3.1 电机持续转动
        2. 7.5.3.2 电机初始未转动
      4. 7.5.4 2006 错误
    6. 7.6 不易识别惯性的应用
      1. 7.6.1 自动泵（齿槽力大/摩擦力大）
      2. 7.6.2 直接驱动型洗衣机（额定转速低且反电势大）
      3. 7.6.3 压缩机（启动电流大）
  9. 8 MCU 注意事项
    1. 8.1 概述
    2. 8.2 支持 InstaSPIN 的器件
      1. 8.2.1 softwareUpdate1p6() - 用户代码中所需的函数
    3. 8.3 ROM 和用户内存概述
      1. 8.3.1 ROM 中的 InstaSPIN-FOC™ 完全执行
        1. 8.3.1.1 从 ROM 和 RAM 中执行
        2. 8.3.1.2 从 ROM 和闪存中执行
      2. 8.3.2 ROM 中的 InstaSPIN-FOC™ 最小实现
        1. 8.3.2.1 从 ROM 和 RAM 中执行
        2. 8.3.2.2 从 ROM 和闪存中执行
      3. 8.3.3 ROM 中的 InstaSPIN-MOTION™
        1. 8.3.3.1 在主中断内执行 InstaSPIN™-MOTION
        2. 8.3.3.2 从 RAM 中执行库
        3. 8.3.3.3 从闪存中执行库
    4. 8.4 关于 CPU 负载和内存占用量测量的详细信息
      1. 8.4.1 CPU 利用率测量详情
      2. 8.4.2 内存分配测量详情
      3. 8.4.3 在 ROM 中构建 IQmath
      4. 8.4.4 堆栈利用率测量详情
      5. 8.4.5 InstaSPIN™ 主中断
      6. 8.4.6 时钟速率
    5. 8.5 内存占用量
      1. 8.5.1 器件内存映射
        1. 8.5.1.1 F2806xF 和 F2806xM 器件
        2. 8.5.1.2 F2805xF 和 F2805xM 器件
        3. 8.5.1.3 F2802xF 器件
      2. 8.5.2 InstaSPIN™ 内存占用量
        1. 8.5.2.1 F2806xF 和 F2805xF 器件
        2. 8.5.2.2 F2802xF 器件
        3. 8.5.2.3 F2806xM 和 F2805xM 器件
      3. 8.5.3 内存等待状态
        1. 8.5.3.1 F2806xF/M 器件
        2. 8.5.3.2 F2805xF/M 器件
        3. 8.5.3.3 F2802xF 器件
      4. 8.5.4 用于仅 RAM 执行的所需闪存配置
      5. 8.5.5 只执行内存的调试 (IDE)
    6. 8.6 CPU 负载
      1. 8.6.1 F2806xF 器件
        1. 8.6.1.1 CPU 周期数
          1. 8.6.1.1.1 RAM 中的用户代码
            1. 8.6.1.1.1.1 完全执行
            2. 8.6.1.1.1.2 最小执行
          2. 8.6.1.1.2 闪存中的用户代码
            1. 8.6.1.1.2.1 完全执行
            2. 8.6.1.1.2.2 最小执行
        2. 8.6.1.2 PWM = 10kHz 时的 CPU 负载
        3. 8.6.1.3 PWM = 20kHz 时的 CPU 负载
        4. 8.6.1.4 CPU 负载示例
          1. 8.6.1.4.1 F2806xF 器件示例 1
          2. 8.6.1.4.2 F2806xF 器件示例 2
      2. 8.6.2 F2806xM 器件
        1. 8.6.2.1 CPU 周期数
          1. 8.6.2.1.1 RAM 执行 - SpinTAC™ 库和用户代码
          2. 8.6.2.1.2 闪存执行 - SpinTAC™ 库和用户代码
        2. 8.6.2.2 CPU 负载示例
          1. 8.6.2.2.1 F2806xM 器件示例 1
          2. 8.6.2.2.2 F2806xM 器件示例 2
          3. 8.6.2.2.3 F2806xM 器件示例 3
          4. 8.6.2.2.4 F2806xM 器件示例 4（SpinTAC™ 位置）
      3. 8.6.3 F805xF 器件
        1. 8.6.3.1 CPU 周期数
        2. 8.6.3.2 PWM = 10kHz 时的 CPU 负载
        3. 8.6.3.3 PWM = 20kHz 时的 CPU 负载
      4. 8.6.4 F2805xM 器件
        1. 8.6.4.1 CPU 周期数
          1. 8.6.4.1.1 闪存执行 - SpinTAC™ 库和用户代码
      5. 8.6.5 F2802xF 器件
        1. 8.6.5.1 CPU 周期数
        2. 8.6.5.2 PWM = 10kHz 时的 CPU 负载
        3. 8.6.5.3 PWM = 20kHz 时的 CPU 负载
    7. 8.7 数字和模拟引脚
      1. 8.7.1 引脚利用率
      2. 8.7.2 F2805x 模拟前端 (AFE)
        1. 8.7.2.1 AFE 模块注意事项
        2. 8.7.2.2 电流信号传输
        3. 8.7.2.3 基准电压连接
        4. 8.7.2.4 电压信号传输
  10. 9 实时结构
    1. 9.1 InstaSPIN™ 软件执行时钟树
    2. 9.2 用于实时调度的软件抽取
      1. 9.2.1 USER_NUM_ISR_TICKS_PER_CTRL_TICK
      2. 9.2.2 USER_NUM_CTRL_TICKS_PER_CURRENT_TICK
      3. 9.2.3 USER_NUM_CTRL_TICKS_PER_EST_TICK
      4. 9.2.4 实例
      5. 9.2.5 USER_NUM_CTRL_TICKS_PER_SPEED_TICK
      6. 9.2.6 USER_NUM_CTRL_TICKS_PER_TRAJ_TICK
    3. 9.3 硬件抽取
  11. 10管理启动时间
    1. 10.1 同时启用偏移和 Rs 重校准功能的启动
    2. 10.2 仅启用偏移重校准时的启动
    3. 10.3 启用 Rs 重校准时的启动
    4. 10.4 不启用任何重校准时的启动
    5. 10.5 忽略惯性估算
  12. 11调整稳压器
    1. 11.1 PI 控制器简介
    2. 11.2 电流控制器的 PI 设计
    3. 11.3 速度控制器的 PI 设计
    4. 11.4 根据稳定性和带宽计算 PI 增益
    5. 11.5 根据阻尼因子计算速度和电流 PI 增益
    6. 11.6 向速度环路添加极点时的考量
    7. 11.7 速度 PI 控制器注意事项：电流限制、钳位和惯性
    8. 11.8 为 FOC 系统设计 PI 控制器时的注意事项
      1. 11.8.1 电机类型间的 FOC 差异
      2. 11.8.2 Q 轴与 D 轴间的耦合
    9. 11.9 采样和数字系统考量
      1. 11.9.1 积分增益中的采样周期考量
      2. 11.9.2 数字格式考量
      3. 11.9.3 PI 系数换算考量
  13. 12InstaSPIN-MOTION™ 控制器
    1. 12.1 概述
    2. 12.2 稳定性
      1. 12.2.1 稳定性量化分析
        1. 12.2.1.1 SpinTAC™ 速度控制稳定性
        2. 12.2.1.2 SpinTAC™ 位置控制稳定性
      2. 12.2.2 性能
        1. 12.2.2.1 频域分析
        2. 12.2.2.2 时域分析
      3. 12.2.3 稳定性和性能之间的权衡
      4. 12.2.4 调整 SpinTAC™ 控制器
        1. 12.2.4.1 注意事项
        2. 12.2.4.2 调整 InstaSPIN™-MOTION 控制器
    3. 12.3 SpinTAC™ 速度控制的软件配置
      1. 12.3.1 包括头文件
      2. 12.3.2 声明全局结构
      3. 12.3.3 初始化配置变量
      4. 12.3.4 调用 SpinTAC™ 速度控制
      5. 12.3.5 SpinTAC™ 速度控制故障排除
        1. 12.3.5.1 ERR_ID
    4. 12.4 速度控制中的最优性能
      1. 12.4.1 简介
      2. 12.4.2 比较速度控制器
      3. 12.4.3 抗扰
      4. 12.4.4 系统配置跟踪
      5. 12.4.5 InstaSPIN-MOTION™ 速度控制优势
        1. 12.4.5.1 单个参数调整
        2. 12.4.5.2 抗扰测试
        3. 12.4.5.3 前馈
        4. 12.4.5.4 无积分器饱和
        5. 12.4.5.5 最小启动过冲
        6. 12.4.5.6 结论
    5. 12.5 SpinTAC™ 位置控制的软件配置
      1. 12.5.1 包括头文件
      2. 12.5.2 声明全局结构
      3. 12.5.3 初始化配置变量
      4. 12.5.4 调用 SpinTAC™ 位置控制
      5. 12.5.5 SpinTAC™ 位置控制故障排除
        1. 12.5.5.1 ERR_ID
    6. 12.6 位置控制中的出色性能
      1. 12.6.1 简介
      2. 12.6.2 比较位置控制器
      3. 12.6.3 抗扰
      4. 12.6.4 系统配置跟踪
      5. 12.6.5 InstaSPIN-MOTION™ 位置控制优势
        1. 12.6.5.1 单个参数调整
        2. 12.6.5.2 抗扰
        3. 12.6.5.3 前馈
        4. 12.6.5.4 低速运行和平滑启动
        5. 12.6.5.5 最小阶跃响应稳定时间
        6. 12.6.5.6 结论
  14. 13轨迹规划
    1. 13.1 生成 InstaSPIN-MOTION™ 系统配置
      1. 13.1.1 急动对系统性能的影响
    2. 13.2 SpinTAC™ 速度移动的软件配置
      1. 13.2.1 包括头文件
      2. 13.2.2 声明全局结构
      3. 13.2.3 初始化配置变量
      4. 13.2.4 调用 SpinTAC™ 速度移动
      5. 13.2.5 SpinTAC™ 速度移动故障排除
        1. 13.2.5.1 ERR_ID
    3. 13.3 SpinTAC™ 位置移动的软件配置
      1. 13.3.1 包括头文件
      2. 13.3.2 声明全局结构
      3. 13.3.3 初始化配置变量
      4. 13.3.4 调用 SpinTAC™ 位置移动
      5. 13.3.5 SpinTAC™ 位置移动疑难解答
        1. 13.3.5.1 位置系统配置限制
        2. 13.3.5.2 ERR_ID
    4. 13.4 InstaSPIN-MOTION™ 序列计划
      1. 13.4.1 SpinTAC™ 速度规划元素
        1. 13.4.1.1 状态
        2. 13.4.1.2 转换
        3. 13.4.1.3 工作条件
        4. 13.4.1.4 变量
        5. 13.4.1.5 操作
      2. 13.4.2 SpinTAC™ 速度规划元素限制
        1. 13.4.2.1 确定 SpinTAC™ 速度规划配置数组大小的示例
      3. 13.4.3 SpinTAC™ 速度规划示例：洗衣机搅动
      4. 13.4.4 SpinTAC™ 速度规划示例：车库门
      5. 13.4.5 SpinTAC™ 速度规划示例：洗衣机
      6. 13.4.6 SpinTAC™ 位置规划示例：售货机
    5. 13.5 SpinTAC™ 速度规划的软件配置
      1. 13.5.1 包括头文件
      2. 13.5.2 定义配置数组的大小
      3. 13.5.3 声明全局结构
      4. 13.5.4 初始化配置变量
      5. 13.5.5 调用 SpinTAC™ 速度规划
      6. 13.5.6 调用 SpinTAC™ 速度规划节拍
      7. 13.5.7 根据 SpinTAC™ 速度移动状态更新 SpinTAC™ 速度规划
    6. 13.6 SpinTAC™ 速度规划疑难解答
      1. 13.6.1 ERR_ID
      2. 13.6.2 配置错误
    7. 13.7 SpinTAC™ 位置规划的软件配置
      1. 13.7.1 包括头文件
      2. 13.7.2 定义配置数组的大小
      3. 13.7.3 声明全局结构
      4. 13.7.4 初始化配置变量
      5. 13.7.5 调用 SpinTAC™ 位置规划
      6. 13.7.6 调用 SpinTAC™ 位置规划节拍
      7. 13.7.7 根据 SpinTAC™ 位置移动状态更新 SpinTAC™ 位置规划
    8. 13.8 SpinTAC™ 位置计划故障排除
      1. 13.8.1 ERR_ID
      2. 13.8.2 配置错误
    9. 13.9 结论
  15. 14管理启动、低速和换向时的满负载
    1. 14.1 概述
    2. 14.2 满载低速运行
      1. 14.2.1 满载低速运行时的考量
        1. 14.2.1.1 启用偏移重校准
        2. 14.2.1.2 启用定子 Rs 重校准
        3. 14.2.1.3 禁用强制角
        4. 14.2.1.4 调整速度控制器以避免电机停转
        5. 14.2.1.5 调整电压反馈电路
      2. 14.2.2 瞬时满载低速运行示例
        1. 14.2.2.1 4Hz，无负载至满载瞬态
        2. 14.2.2.2 2Hz，无负载至满载瞬态
    3. 14.3 满载换向
      1. 14.3.1 满载低速运行时的换向考量
      2. 14.3.2 满载低速运行时的换向示例
        1. 14.3.2.1 满载情况下从 -4 至 +4Hz
        2. 14.3.2.2 满载情况下从 -2 至 +2 Hz
    4. 14.4 满载电机启动
      1. 14.4.1 满载电机启动的考量
        1. 14.4.1.1 启用强制角
      2. 14.4.2 满载电机启动示例
        1. 14.4.2.1 满载情况下从静止至 4Hz
        2. 14.4.2.2 满载情况下从静止至 2Hz
    5. 14.5 满载从静止状态快速加速
      1. 14.5.1 无需电机对准时满载最快速度启动电机的考量
        1. 14.5.1.1 加载有效偏移并禁用偏移重校准
        2. 14.5.1.2 加载有效 Rs 并禁用 Rs 重校准
        3. 14.5.1.3 无需电机对准时满载最快速度启动电机的示例
      2. 14.5.2 需要电机对准时满载最快速度启动电机的考量
        1. 14.5.2.1 最大化电流斜率
        2. 14.5.2.2 需要电机对准时满载最快速度启动电机的示例
    6. 14.6 过载和电机过热
      1. 14.6.1 过载和电机过热的考量
      2. 14.6.2 过载和电机过热示例
    7. 14.7 InstaSPIN-MOTION™ 和低速运行的考量
  16. 15Rs 在线重校准
    1. 15.1  概要
    2. 15.2  电阻与温度之间的关系
    3. 15.3  低速运行（包括启动）时所需的 Rs 准确值
    4. 15.4  Rs 在线重校准介绍
    5. 15.5  Rs 在线重校准与 Rs 离线重校准
    6. 15.6  启用 Rs 在线重校准
    7. 15.7  禁用 Rs 在线重校准
    8. 15.8  修改 Rs 在线参数
      1. 15.8.1 调整注入电流幅度
      2. 15.8.2 调整慢速转角
      3. 15.8.3 调整 Rs 在线值递增和递减的增量
      4. 15.8.4 调整滤波器参数
    9. 15.9  监控 Rs 在线电阻值
      1. 15.9.1 Rs 在线浮点值
      2. 15.9.2 Rs 在线定点值
    10. 15.10 使用 Rs 在线特性作为温度传感器
    11. 15.11 Rs 在线特性相关状态框图（CTRL 和 EST）
  17. 16PowerWarp™
    1. 16.1 概述
    2. 16.2 启用 PowerWarp™ 软件
    3. 16.3 PowerWarp™ 电流斜率
    4. 16.4 实例
    5. 16.5 案例研究
  18. 17分流电流测量
    1. 17.1 简介
    2. 17.2 信号
    3. 17.3 1 分流
    4. 17.4 2 分流
    5. 17.5 3 分流
    6. 17.6 开发套件
      1. 17.6.1 DRV8312 套件
      2. 17.6.2 DRV8301 套件
    7. 17.7 结论
  19. 18传感系统
    1. 18.1 正交编码器的硬件配置
      1. 18.1.1 引脚用量
    2. 18.2 正交编码器的软件配置
      1. 18.2.1 针对 EQEP 操作配置电机
      2. 18.2.2 初始化 EQEP 句柄
      3. 18.2.3 设置数字 IO 以连接 QEP 外设
      4. 18.2.4 启用 eQEP 时钟
      5. 18.2.5 初始化 ENC 模块
      6. 18.2.6 设置 ENC 模块
      7. 18.2.7 调用 eQEP 函数
      8. 18.2.8 为 FOC 提供 eQEP 角度
    3. 18.3 InstaSPIN-MOTION™ 位置转换
      1. 18.3.1 SpinTAC™ 位置转换的软件配置
        1. 18.3.1.1 包括头文件
        2. 18.3.1.2 声明全局结构
        3. 18.3.1.3 初始化配置变量
        4. 18.3.1.4 调用 SpinTAC™ 位置转换
      2. 18.3.2 SpinTAC™ 位置转换疑难解答
        1. 18.3.2.1 ERR_ID
  20.   A 术语和缩略词定义
  21.   B 修订历史记录

11.2 电流控制器的 PI 设计

上一节中我们简单回顾了 PI 控制器的历史，还介绍了现在常用的两种拓扑形式。无论使用哪种形式，频率响应都相同，如图 12-4 所示。从图中可以看出，PI 控制器的增益对系统稳定性有显著的影响。但这也说明图中的拐点（“零点”频率）对系统性能起重要作用，只不过这种作用可能比较难以理解。要弄清楚这一点，我们必须借助数学手段导出 PI 控制器的传递函数，然后了解控制器的“零点”在整个系统响应中如何发挥作用。

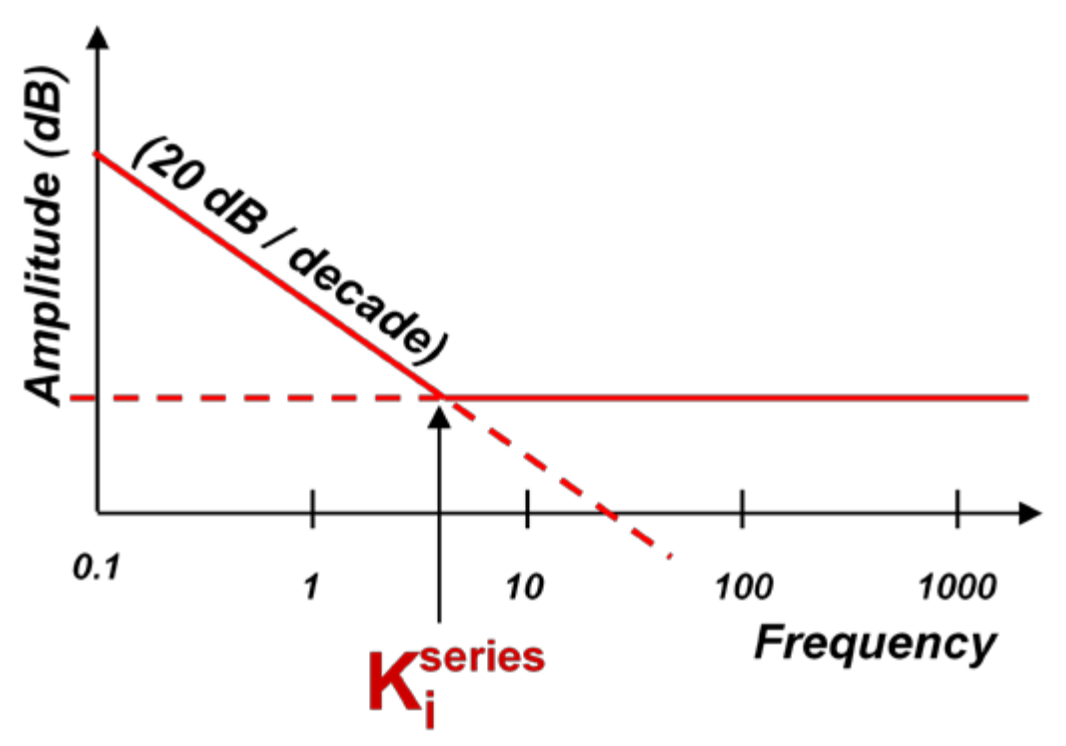GUID-22B4DD64-7877-4F3F-A22B-19A31A49EA78-low.png图 11-4 频率响应

使用串联形式的 PI 控制器，我们可将从误差信号到控制器输出的“s 域”传递函数定义为：

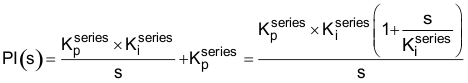
Equation28. GUID-0F06ABEA-34BC-4CDB-A84E-67D2ACD9841A-low.gif

根据该表达式，我们可以清楚地看到 s = 0 时为极点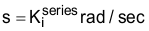，GUID-A15959AC-1D19-41D6-AC13-BAB1644D2230-low.gif 时为零点。那么，该零点值为什么如此重要？要回答这个问题，让我们将 PI 控制器放入用于调节电机电流的电流控制器，如图 12-5 所示。

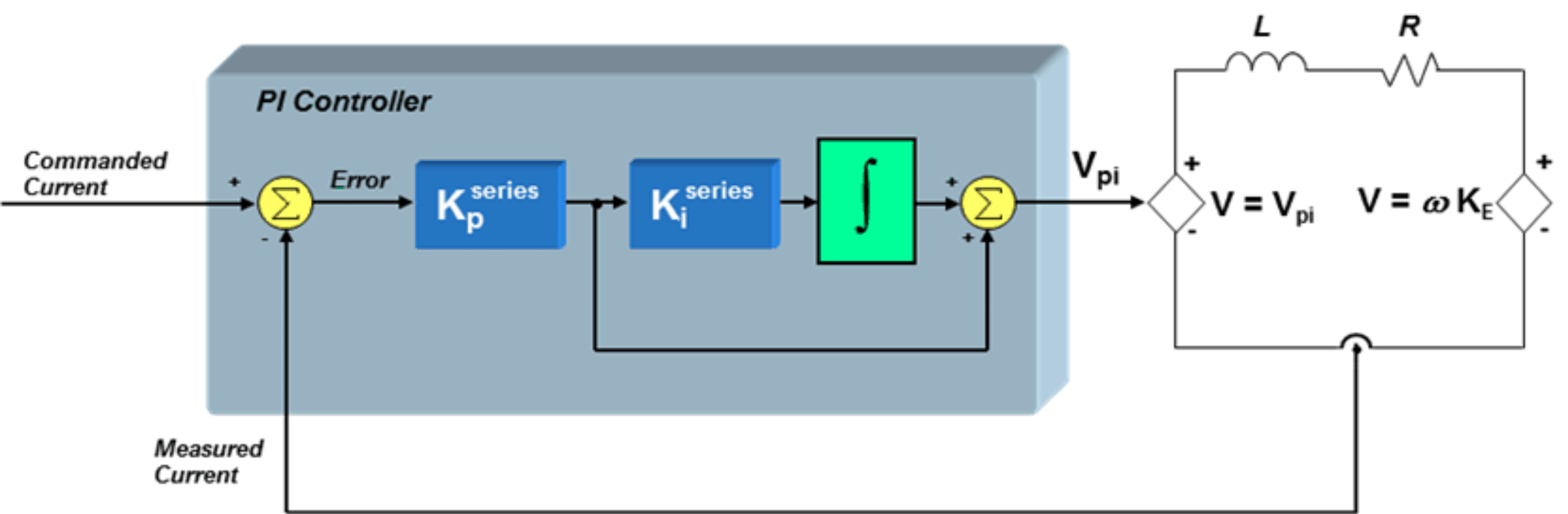GUID-C5FB4C8F-C81B-4663-A5B9-35E3BF4633F8-low.png图 11-5 电流控制器中的 PI 控制器

我们将电机绕组近似看作简单一阶串联电路，该电路中包含电阻器、电感器和反电势电压源。假设现在反电势电压为常数（因为通常相对于电流来说反电势电压变化缓慢），我们可将从电机电压到电机电流的小信号传递函数定义为：

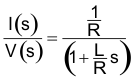
Equation29. GUID-5EE3D655-E6FB-4203-8ACA-57E100543320-low.gif

如果我们还假设 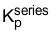GUID-6D5B57E6-F2FE-40D8-A092-23FD5C2554A6-low.gif 项中包括总线电压和 PWM 增益调节，则可将“环路增益”定义为 PI 控制器传递函数和 RL 电路中 V-I 传递函数的乘积：

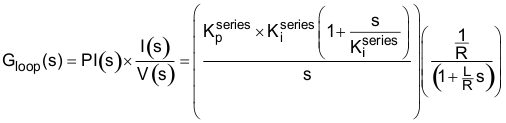
Equation30. GUID-2E371BC2-1700-4225-AAE9-8C20FC3825F6-low.gif

为了确定系统总响应（闭环增益），我们必须使用以下表达式，这些表达式您在大学控制系统课程中见到过：

Equation31. GUID-50A62769-4460-4871-963E-0CBFC7E7BBB8-low.gif

将Equation30 代入Equation31 得到：

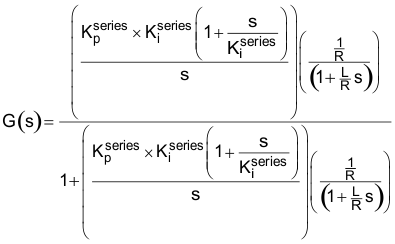
Equation32. GUID-4BAF7984-4363-48E3-BF0B-FDDBB48B0ACF-low.gif

请注意，表达式越来越复杂，但通过一些代数变换可将表达式简化为下式：

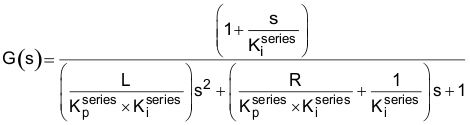
Equation33. GUID-26A33CBF-2F89-4191-98AC-8CFE2E442141-low.gif

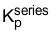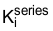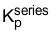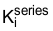分母是“s”的二阶表达式，表示传递函数中存在两个极点。如果我们不谨慎选择 GUID-6D5B57E6-F2FE-40D8-A092-23FD5C2554A6-low.gif 和 GUID-1A1D7507-C3DF-454A-9DBC-CCDB2A345322-low.gif，则容易在最后得出复极点。根据复极点与 jω 轴的靠近程度，系统可能会出现一些谐振峰。因此我们可立即假设，要选择的 GUID-6D5B57E6-F2FE-40D8-A092-23FD5C2554A6-low.gif 和 GUID-1A1D7507-C3DF-454A-9DBC-CCDB2A345322-low.gif 可避免存在复极点。也就是说，我们可以将分母表示为以下表达式，其中 C 和 D 为实数：

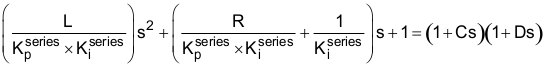
Equation34. GUID-B4B14171-92D8-4E2D-8A96-791B50A14FF6-low.gif

如果将方程右侧的表达式乘开，将结果与方程左侧的表达式进行比较，可以看到要想得到实极点，必须满足以下条件：

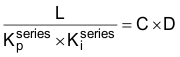
Equation35. GUID-75CDB97F-39B4-4C5F-8234-8F3743700F80-low.gif

和：

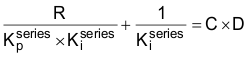
Equation36. GUID-9B31FAF9-4146-4AF6-977D-20BC89D3AB64-low.gif

作为解Equation35 和Equation36 的第一步，只需要使Equation36 两侧的各项相等。即：

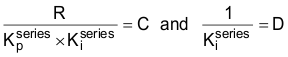
Equation37. GUID-CE21DD4B-3A63-4456-B3E0-FCA12C29E3BC-low.gif

我们马上就会了解进行上述替换的原因。如果用Equation34 中所示的等效表达式替换Equation33 的分母，然后再进行Equation37 中建议的替换，则得到：

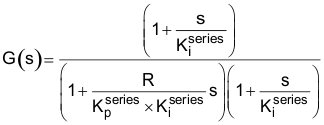
Equation38. GUID-5AE097D8-2128-4B59-B147-E5D391DAA8CB-low.gif

请注意，替换“D”可导致在闭环增益表达式中得到极点而不会产生零点。通过正确选择 C 和 D，我们不但最终会得到实极点，而且生成的闭环系统响应只有一个实极点而无零点。无尖峰频率响应或谐振情况，只是简单的单极点低通响应。

此外，通过将Equation37 中建议的 C 和 D 表达式替换回Equation35，可得到下列等式：

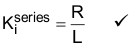
Equation39. GUID-CD0A75CC-4E55-4AFF-B213-21A7E0D23D47-low.gif

请记住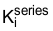，GUID-1A1D7507-C3DF-454A-9DBC-CCDB2A345322-low.gif 是出现控制器零点时的频率。因此，为了得到Equation38 所描述的响应，我们需要做的是将 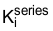GUID-1A1D7507-C3DF-454A-9DBC-CCDB2A345322-low.gif（控制器零点频率）设置为设备极点。

现在我们已经知道如何设置 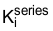GUID-1A1D7507-C3DF-454A-9DBC-CCDB2A345322-low.gif。但如何设置 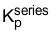GUID-6D5B57E6-F2FE-40D8-A092-23FD5C2554A6-low.gif 呢？下面重写闭环系统响应 G(s) 的表达式，进行上述所有替换，将得到以下表达式：

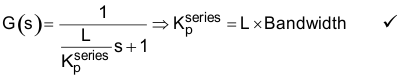
Equation40. GUID-B985C7F3-A860-4250-8A46-4272EEC1EDF5-low.gif

总体来说，有一些简单的规则可以帮助您设计电流环路的 PI 控制器：

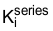GUID-1A1D7507-C3DF-454A-9DBC-CCDB2A345322-low.gif 可设定 PI 控制器的零点。当控制自身传递函数中只有一个实极点的设备参数时（如电机中的电流），应将 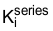GUID-1A1D7507-C3DF-454A-9DBC-CCDB2A345322-low.gif 设为该实极点的值。这样可消除极点/零点并生成同样只有单个实极点的闭环响应。即非常稳定、不含谐振峰的响应。

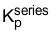GUID-6D5B57E6-F2FE-40D8-A092-23FD5C2554A6-low.gif 可设定闭环系统响应的带宽。如Equation40 所示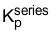，GUID-6D5B57E6-F2FE-40D8-A092-23FD5C2554A6-low.gif 越大，电流环路带宽越大。我们将在后面的章节中讨论如何选择合适的带宽。无论选择的带宽频率是多少，都可能会出现 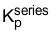GUID-6D5B57E6-F2FE-40D8-A092-23FD5C2554A6-low.gif 等于电感阻抗的情况。

在下一节中，我们将讨论如何设计将 PI 电流控制器作为内部环路的级联 PI 速度环路。
千亿体育app官网登录(中国)官方网站IOS/安卓通用版/手机APP | 米乐app下载官网（中国）|ios|Android/通用版APP最新版 | 米乐|米乐·M6（中国大陆）官方网站 | 千亿体育登陆地址 | 华体会体育（中国）HTH·官方网站 | 千赢qy国际_全站最新版千赢qy国际V6.2.14安卓/IOS下载 | 18新利网v1.2.5|中国官方网站 | bob电竞真人（中国官网）安卓/ios苹果/电脑版【1.97.95版下载】 | 千亿体育app官方下载(中国)官方网站IOS/安卓/手机APP下载安装 |