ZHCU083I January   2013  – October 2021 TMS320F2802-Q1 , TMS320F28026-Q1 , TMS320F28026F , TMS320F28027-Q1 , TMS320F28027F , TMS320F28027F-Q1 , TMS320F28052-Q1 , TMS320F28052F , TMS320F28052F-Q1 , TMS320F28052M , TMS320F28052M-Q1 , TMS320F28054-Q1 , TMS320F28054F , TMS320F28054F-Q1 , TMS320F28054M , TMS320F28054M-Q1 , TMS320F2806-Q1 , TMS320F28062-Q1 , TMS320F28062F , TMS320F28062F-Q1 , TMS320F28068F , TMS320F28068M , TMS320F28069-Q1 , TMS320F28069F , TMS320F28069F-Q1 , TMS320F28069M , TMS320F28069M-Q1

 

  1.   Read This First
    1.     关于本手册
    2.     术语表
    3.     支持资源
    4.     商标
  2. 1 引言
    1. 1.1 InstaSPIN-FOC™ 和 FAST™ 概述
      1. 1.1.1 FAST™ 估算器特性
      2. 1.1.2 InstaSPIN-FOC™ 解决方案特性
      3. 1.1.3 InstaSPIN-FOC™ 方框图
      4. 1.1.4 将 FAST™ 估算器与典型解决方案相比较
      5. 1.1.5 FAST™ 提供无传感器 FOC 性能
        1. 1.1.5.1 FAST 估算器取代机械传感器
        2. 1.1.5.2 对性能十分关键的转子角准确度
    2. 1.2 InstaSPIN-MOTION™ 和 SpinTAC™ 概述
      1. 1.2.1 InstaSPIN-MOTION™ 关键功能和优势
        1. 1.2.1.1 FAST 统一软件观测器
        2. 1.2.1.2 SpinTAC 运动控制套件
          1. 1.2.1.2.1 IDENTIFY
          2. 1.2.1.2.2 CONTROL
          3. 1.2.1.2.3 MOVE
          4. 1.2.1.2.4 PLAN
        3. 1.2.1.3 其他 InstaSPIN-MOTION 特性
      2. 1.2.2 InstaSPIN-MOTION™ 方框图
      3. 1.2.3 应用示例
        1. 1.2.3.1 跑步机传送带：不同速度和负载下的平滑运动
        2. 1.2.3.2 摄像机：低速时的平滑运动和位置精度
        3. 1.2.3.3 洗衣机：低速时的平滑运动和位置准确度
          1. 1.2.3.3.1 搅动周期
          2. 1.2.3.3.2 旋转周期
          3. 1.2.3.3.3 InstaSPIN-MOTION 在整个工作范围内的运行
  3. 2 快速入门套件 - TI 提供的软件和硬件
    1. 2.1 概述
    2. 2.2 评估 InstaSPIN-FOC™ 和 InstaSPIN-MOTION™
  4. 3 InstaSPIN™ 和 MotorWare™
    1. 3.1 概述
    2. 3.2 MotorWare™ 目录结构
      1. 3.2.1 MotorWare™ – 驱动程序
      2. 3.2.2 MotorWare™ – ide
      3. 3.2.3 MotorWare™ – modules
      4. 3.2.4 MotorWare™ – solutions（解决方案）
    3. 3.3 MotorWare™ 面向对象的设计
      1. 3.3.1 对象
      2. 3.3.2 方法
        1. 3.3.2.1 Init 方法
        2. 3.3.2.2 Set 方法
        3. 3.3.2.3 Get 方法
        4. 3.3.2.4 Run 方法
    4. 3.4 InstaSPIN-FOC™ API
      1. 3.4.1 控制器 API 函数 - ctrl.c、ctrl.h、CTRL_obj.h
        1. 3.4.1.1 CTRL 枚举和结构
          1.        CTRL_Obj
          2.        CTRL_State_e
          3.        CTRL_ErrorCode_e
          4.        CTRL_TargetProc_e
          5.        CTRL_Type_e
          6.        CTRL_Version
        2. 3.4.1.2 CTRL 状态控制和错误处理
          1.        CTRL_initCtrl()
          2.        CTRL_updateState ()
          3.        CTRL_isError ()
          4.        CTRL_checkForErrors ()
        3. 3.4.1.3 CTRL Get 函数
          1.        CTRL_getCount_current ()
          2.        CTRL_getCount_isr ()
          3.        CTRL_getCount_speed ()
          4.        CTRL_getCount_state ()
          5.        CTRL_getCount_traj ()
          6.        CTRL_getCtrlFreq ()
          7.        CTRL_getCtrlPeriod_sec ()
          8.        CTRL_getErrorCode ()
          9.        CTRL_getEstHandle ()
          10.        CTRL_getFlag_enableCtrl ()
          11.        CTRL_getFlag_enableDcBusComp ()
          12.        CTRL_getFlag_enablePowerWarp ()
          13.        CTR CTRL_getFlag_enableOffset ()
          14.        CTRL_getFlag_enableSpeedCtrl ()
          15.        CTRL_getFlag_enableUserMotorParams ()
          16.        CTRL_getGains ()
          17.        CTRL_getIab_filt_pu ()
          18.        CTRL_getIab_filt_addr ()
          19.        CTRL_getIab_in_addr ()
          20.        CTRL_getIab_in_pu ()
          21.        CTRL_getId_in_pu ()
          22.        CTRL_getId_ref_pu ()
          23.        CTRL_getIdq_in_addr ()
          24.        CTRL_getIdq_in_pu ()
          25.        CTRL_getIdq_ref_pu ()
          26.        CTRL_getIdRated_pu ()
          27.        CTRL_getIq_in_pu ()
          28.        CTRL_getIq_ref_pu ()
          29.        CTRL_getKi ()
          30.        CTRL_getKd ()
          31.        CTRL_getKp ()
          32.        CTRL_getLhf ()
          33.        CTRL_getMagCurrent_pu ()
          34.        CTRL_getMaxVsMag_pu ()
          35.        CTRL_getMaximumSpeed_pu ()
          36.        CTRL_getMotorRatedFlux ()
          37.        CTRL_getMotorType ()
          38.        CTRL_getNumCtrlTicksPerCurrentTick ()
          39.        CTRL_getNumCtrlTicksPerSpeedTick ()
          40.        CTRL_getNumCtrlTicksPerTrajTick ()
          41.        CTRL_getNumIsrTicksPerCtrlTick ()
          42.        CTRL_getRefValue_pu ()
          43.        CTRL_getRhf ()
          44.        CTRL_getRoverL ()
          45.        CTRL_getSpd_max_pu ()
          46.        CTRL_getSpd_out_addr ()
          47.        CTRL_getSpd_out_pu ()
          48.        CTRL_getSpd_ref_pu ()
          49.        CTRL_getSpd_int_ref_pu ()
          50.        CTRL_getState ()
          51.        CTRL_getTrajFreq ()
          52.        CTRL_getTrajPeriod_sec ()
          53.        CTRL_getTrajStep ()
          54.        CTRL_getUi ()
          55.        CTRL_getVab_in_pu ()
          56.        CTRL_getVab_out_addr ()
          57.        CTRL_getVab_out_pu ()
          58.        CTRL_getVd_out_addr ()
          59.        CTRL_getVd_out_pu ()
          60.        CTRL_getVdq_out_addr ()
          61.        CTRL_getVdq_out_pu ()
          62.        CTRL_getVersion ()
          63.        CTRL_getVq_out_addr ()
          64.        CTRL_getVq_out_pu ()
          65.        CTRL_getWaitTime ()
        4. 3.4.1.4 CTRL 计数器函数
          1.        CTRL_incrCounter_current ()
          2.        CTRL_incrCounter_isr ()
          3.        CTRL_incrCounter_speed ()
          4.        CTRL_incrCounter_state ()
          5.        CTRL_incrCounter_traj ()
          6.        CTRL_resetCounter_current ()
          7.        CTRL_resetCounter_isr ()
          8.        CTRL_resetCounter_speed ()
          9.        CTRL_resetCounter_state ()
          10.        CTRL_resetCounter_traj ()
        5. 3.4.1.5 CTRL Set 函数
          1.        CTRL_setCtrlFreq_Hz ()
          2.        CTRL_setCtrlFreq_sec ()
          3.        CTRL_setErrorCode ()
          4.        CTRL_setEstParams ()
          5.        CTRL_setFlag_enableCtrl ()
          6.        CTRL_setFlag_enableDcBusComp ()
          7.        CTRL_setFlag_enablePowerWarp ()
          8.        CTRL_setFlag_enableOffset ()
          9.        calibrationCTRL_setFlag_enableSpeedCtrl ()
          10.        CTRL_setFlag_enableUserMotorParams ()
          11.        CTRL_setGains ()
          12.        CTRL_setIab_in_pu ()
          13.        CTRL_setIab_filt_pu ()
          14.        CTRL_setId_ref_pu ()
          15.        CTRL_setIdq_in_pu ()
          16.        CTRL_setIdq_ref_pu ()
          17.        CTRL_setIdRated_pu ()
          18.        CTRL_setIq_ref_pu ()
          19.        CTRL_setKd ()
          20.        CTRL_setKi ()
          21.        CTRL_setKp ()
          22.        CTRL_setLhf ()
          23.        CTRL_setMagCurrent_pu ()
          24.        CTRL_setMaxVsMag_pu ()
          25.        CTRL_setMaxAccel_pu ()
          26.        CTRL_setMaximumSpeed_pu ()
          27.        CTRL_setParams()
          28.        CTRL_setNumCtrlTicksPerCurrentTick ()
          29.        CTRL_setNumCtrlTicksPerSpeedTick ()
          30.        CTRL_setNumCtrlTicksPerTrajTick ()
          31.        CTRL_setNumIsrTicksPerCtrlTick ()
          32.        CTRL_setRhf ()
          33.        CTRL_setRoverL ()
          34.        CTRL_setSpdMax ()
          35.        CTRL_setSpd_max_pu ()
          36.        CTRL_setSpd_out_pu ()
          37.        CTRL_setSpd_ref_pu ()
          38.        CTRL_setSpd_ref_krpm ()
          39.        CTRL_setState ()
          40.        CTRL_setTrajFreq_Hz ()
          41.        CTRL_setTrajPeriod_sec ()
          42.        CTRL_setUi ()
          43.        CTRL_setupClarke_I ()
          44.        CTRL_setupClarke_V ()
          45.        CTRL_setupEstIdleState ()
          46.        CTRL_setupEstOnLineState ()
          47.        CTRL_setUserMotorParams ()
          48.        CTRL_setVab_in_pu ()
          49.        CTRL_setVab_out_pu ()
          50.        CTRL_setVdq_out_pu ()
          51.        CTRL_setWaitTimes ()
          52.        CTRL_setup ()
          53.        CTRL_setupCtrl ()
          54.        CTRL_setupEst ()
          55.        CTRL_setupTraj ()
        6. 3.4.1.6 CTRL Run 和 Compute 函数
          1.        CTRL_angleDelayComp ()
          2.        CTRL_computePhasor ()
          3.        CTRL_doCurrentCtrl ()
          4.        CTRL_doSpeedCtrl ()
          5.        CTRL_run()
          6.        CTRL_runTraj ()
          7.        CTRL_runOffLine ()
          8.        CTRL_runOnLine ()
          9.        CTRL_runOnLine_User ()
          10.        CTRL_useZeroIq_ref ()
      2. 3.4.2 估算器 API 函数 - FAST™ 库 - est.h、est_states.h
        1. 3.4.2.1 EST 枚举和结构
          1.        EST_RsOnLineFilterType_e
          2.        EST_ErrorCode_e
          3.        EST_State_e
        2. 3.4.2.2 EST Set 函数
          1.        EST_setRsOnLineId_pu ()
          2.        EST_setAngle_pu ()
          3.        EST_setDcBus_pu ()
          4.        EST_setDir_qFmt ()
          5.        EST_setFe_neg_max_pu ()
          6.        EST_setFe_pos_min_pu ()
          7.        EST_setFlag_enableFluxControl ()
          8.        EST_setFlag_enableForceAngle ()
          9.        EST_setFlag_enableRsOnLine ()
          10.        EST_setFlag_enableRsRecalc ()
          11.        EST_setFlag_estComplete ()
          12.        EST_setFlag_updateRs ()
          13.        EST_setForceAngleDelta_pu ()
          14.        EST_setFreqB0_lp_pu ()
          15.        EST_setFreqBeta_lp_pu ()
          16.        EST_setFullScaleCurrent ()
          17.        EST_setFullScaleFlux ()
          18.        EST_setFullScaleFreq ()
          19.        EST_setFullScaleInductance ()
          20.        EST_setFullScaleResistance ()
          21.        EST_setFullScaleVoltage ()
          22.        EST_setIdle ()
          23.        EST_setIdle_all ()
          24.        EST_setId_ref_pu ()
          25.        EST_setIdRated_pu ()
          26.        EST_setIq_ref_pu ()
          27.        EST_setLs_d_pu ()
          28.        EST_setLs_delta_pu ()
          29.        EST_setLs_dq_pu ()
          30.        EST_setLs_q_pu ()
          31.        EST_setLs_qFmt ()
          32.        EST_setMaxAccel_pu ()
          33.        EST_setMaxAccel_est_pu ()
          34.        EST_setMaxCurrentSlope_pu ()
          35.        EST_setMaxCurrentSlope_PowerWarp_pu ()
          36.        EST_setRr_pu ()
          37.        EST_setRr_qFmt ()
          38.        EST_setRs_delta_pu ()
          39.        EST_setRsOnLine_pu ()
          40.        EST_setRsOnLine_qFmt ()
          41.        EST_setRsOnLineFilterParams ()
          42.        EST_setRsOnLineId_mag_pu ()
          43.        EST_setRs_pu ()
          44.        EST_setRs_qFmt ()
          45.        EST_updateId_ref_pu ()
        3. 3.4.2.3 EST Get 函数
          1.        EST_get_krpm_to_pu_sf ()
          2.        EST_get_pu_to_krpm_sf ()
          3.        EST_getAngle_pu ()
          4.        EST_getDcBus_pu ()
          5.        EST_ErrorCode_e EST_getErrorCode ()
          6.        EST_getFe ()
          7.        EST_getFe_pu ()
          8.        EST_getFlag_enableForceAngle ()
          9.        EST_getFlag_enableRsOnLine ()
          10.        EST_getFlag_enableRsRecalc ()
          11.        EST_getFlag_estComplete ()
          12.        EST_getFlag_updateRs ()
          13.        EST_getFlux_VpHz ()
          14.        EST_getFlux_Wb ()
          15.        EST_getFlux_pu ()
          16.        EST_getFm ()
          17.        EST_getFm_pu ()
          18.        EST_getForceAngleDelta_pu ()
          19.        EST_getForceAngleStatus ()
          20.        EST_getFreqB0_lp_pu ()
          21.        EST_getFreqBeta_lp_pu ()
          22.        EST_getFslip ()
          23.        281
          24.        EST_getFslip_pu ()
          25.        EST_getFullScaleCurrent ()
          26.        EST_getFullScaleFlux ()
          27.        EST_getFullScaleFreq ()
          28.        EST_getFullScaleInductance ()
          29.        EST_getFullScaleResistance ()
          30.        EST_getFullScaleVoltage ()
          31.        EST_getIdRated ()
          32.        EST_getIdRated_pu ()
          33.        EST_getIdRated_indEst_pu ()
          34.        EST_getIdRated_ratedFlux_pu ()
          35.        EST_getLr_H ()
          36.        EST_getLr_pu ()
          37.        EST_getLr_qFmt ()
          38.        EST_getLs_d_H ()
          39.        EST_getLs_d_pu ()
          40.        EST_getLs_delta_pu ()
          41.        EST_getLs_dq_pu ()
          42.        EST_getLs_q_H ()
          43.        EST_getLs_q_pu ()
          44.        EST_getLs_qFmt ()
          45.        EST_getLs_max_pu ()
          46.        EST_getLs_min_pu ()
          47.        EST_getLs_coarse_max_pu ()
          48.        EST_getMaxAccel_pu ()
          49.        EST_getMaxAccel_est_pu ()
          50.        EST_getMaxCurrentSlope_pu ()
          51.        EST_getMaxCurrentSlope_PowerWarp_pu ()
          52.        EST_getOneOverDcBus_pu ()
          53.        EST_getRr_Ohm ()
          54.        EST_getRr_pu ()
          55.        EST_getRr_qFmt ()
          56.        EST_getRs_delta_pu ()
          57.        EST_getRs_Ohm ()
          58.        EST_getRs_pu ()
          59.        EST_getRs_qFmt ()
          60.        EST_getRs_qFmt ()
          61.        EST_getRsOnLine_Ohm ()
          62.        EST_getRsOnLine_pu ()
          63.        EST_getRsOnLineId_mag_pu ()
          64.        EST_getRsOnLineId_pu ()
          65.        EST_getSpeed_krpm ()
          66.        EST_getSignOfDirection ()
          67.        EST_getSpeed_krpm ()
          68.        EST_getState ()
          69.        EST_getTorque_lbin ()
          70.        EST_getTorque_Nm ()
          71.        EST_getDir_qFmt ()
        4. 3.4.2.4 EST Run 和 Compute 函数
          1.        EST_computeLr_H ()
          2.        EST_doCurrentCtrl ()
          3.        EST_genOutputLimits_Pid_Id ()
          4.        EST_genOutputLimits_Pid_Iq ()
          5.        EST_run ()
          6.        EST_computeDirection_qFmt ()
        5. 3.4.2.5 EST 计数器函数
          1.        EST_resetCounter_ctrl ()
          2.        EST_resetCounter_state ()
        6. 3.4.2.6 EST 状态控制和错误处理函数
          1.        EST_isError ()
          2.        EST_isIdle ()
          3.        EST_isLockRotor ()
          4.        EST_isMotorIdentified ()
          5.        EST_isOnLine ()
          6.        EST_updateState ()
          7.        EST_useZeroIq_ref ()
      3. 3.4.3 硬件抽象层 (HAL) API 函数 - hal.c、hal.h、hal_obj.h
        1. 3.4.3.1 HAL 枚举和结构
          1.        HAL_AdcData_t
          2.        HAL_DacData_t
          3.        HAL_PwmData_t
          4.        HAL_LedNumber_e
          5.        GPIO_Number_e
          6.        HAL_SensorType_e
          7.        HAL_Obj
        2. 3.4.3.2 HAL – ADC 和 AFE
          1.        HAL_setupAdcs ()
          2.        HAL_setupAfe ()
          3.        HAL_acqAdcInt ()
          4.        HAL_readAdcData()
          5.        HAL_updateAdcBias ()
          6.        HAL_setBias ()
          7.        HAL_getBias ()
          8.        HAL_cal ()
          9.        HAL_AdcCalConversion ()
          10.        HAL_AdcOffsetSelfCal ()
          11.        HAL_getAdcSocSampleDelay ()
          12.        HAL_setAdcSocSampleDelay ()
          13.        HAL_getCurrentScaleFactor ()
          14.        HAL_setCurrentScaleFactor ()
          15.        HAL_getVoltageScaleFactor ()
          16.        HAL_setVoltageScaleFactor ()
          17.        HAL_getNumCurrentSensors ()
          18.        HAL_setNumCurrentSensors ()
          19.        HAL_getNumVoltageSensors ()
          20.        HAL_setNumVoltageSensors ()
          21.        378
          22.        HAL_getOffsetBeta_lp_pu ()
          23.        HAL_setOffsetBeta_lp_pu ()
          24.        HAL_setOffsetInitCond ()
          25.        HAL_getOffsetValue ()
          26.        HAL_setOffsetValue ()
          27.        HAL_runOffsetEst ()
        3. 3.4.3.3 HAL – PWM 和 PWM-DAC
          1.        HAL_setupPwms ()
          2.        HAL_setupPwmDacs ()
          3.        HAL_readTimerCnt ()
          4.        HAL_reloadTimer ()
          5.        HAL_readPwmPeriod ()
          6.        HAL_disablePwm ()
          7.        HAL_enablePwm ()
          8.        HAL_writeDacData ()
          9.        HAL_writePwmData()
          10.        HAL_readPwmCmpA ()
          11.        HAL_readPwmCmpB ()
          12.        HAL_setTrigger ()
          13.        HAL_acqPwmInt ()
          14.        HAL_enablePwmInt ()
          15.        HAL_hvProtection ()
        4. 3.4.3.4 HAL – CPU 定时器
          1.        HAL_setupClks ()
          2.        HAL_setupTimers ()
          3.        HAL_startTimer ()
          4.        HAL_stopTimer ()
          5.        HAL_setTimerPeriod ()
          6.        HAL_getTimerPeriod ()
        5. 3.4.3.5 HAL – GPIO 和 LED
          1.        HAL_setupGpios ()
          2.        HAL_toggleGpio ()
          3.        HAL_setGpioHigh ()
          4.        HAL_setGpioLow ()
          5.        HAL_toggleLed
        6. 3.4.3.6 HAL – 其他
          1.        HAL_init()
          2.        HAL_initIntVectorTable ()
          3.        HAL_setParams ()
          4.        HAL_setupFlash ()
          5.        HAL_setupPie ()
          6.        HAL_setupPll ()
          7.        HAL_setupPeripheralClks ()
          8.        HAL_getOscTrimValue ()
          9.        HAL_OscTempComp ()
          10.        HAL_osc1Comp ()
          11.        HAL_osc2Comp ()
          12.        HAL_setupFaults ()
          13.        HAL_setParams ()
          14.        HAL_enableDebugInt ()
          15.        HAL_enableGlobalInts ()
          16.        HAL_disableGlobalInts ()
          17.        HAL_disableWdog ()
      4. 3.4.4 用户设置 – user.c、user.h、userParams.h
        1. 3.4.4.1 USER 枚举和结构
          1.        Struct_USER_Params_
          2.        USER_ErrorCode_e
        2. 3.4.4.2 USER Set 和 Compute 函数
          1.        USER_setParams()
          2.        USER_calcPIgains ()
          3.        USER_computeTorque_Ls_Id_Iq_pu_to_Nm_sf ()
          4.        USER_computeTorque_Flux_Iq_pu_to_Nm_sf ()
          5.        USER_computeFlux_pu_to_Wb_sf ()
          6.        USER_computeFlux_pu_to_VpHz_sf ()
          7.        USER_computeFlux ()
          8.        USER_computeTorque_Nm ()
          9.        USER_computeTorque_lbin ()
        3. 3.4.4.3 USER 错误处理函数
          1.        USER_checkForErrors ()
          2.        USER_getErrorCode ()
          3.        USER_setErrorCode ()
      5. 3.4.5 其他函数
        1.       softwareUpdate1p6 ()
    5. 3.5 InstaSPIN-MOTION™ 和 SpinTAC™ API
      1. 3.5.1 头文件、公共库和 ROM 库
      2. 3.5.2 版本信息
        1. 3.5.2.1 返回 SpinTAC™ 版本信息的代码示例
          1. 3.5.2.1.1 包括头文件
          2. 3.5.2.1.2 声明全局结构
          3. 3.5.2.1.3 初始化配置变量
          4. 3.5.2.1.4 返回版本信息
      3. 3.5.3 SpinTAC 结构名称
      4. 3.5.4 SpinTAC™ 变量
    6. 3.6 SpinTAC™ API
      1. 3.6.1 SpinTAC™ 速度控制
        1. 3.6.1.1 SpinTAC™ 速度控制接口
        2. 3.6.1.2 SpinTAC™ 速度控制运行函数
      2. 3.6.2 SpinTAC™ 速度移动
        1. 3.6.2.1 SpinTAC™ 速度移动接口
        2. 3.6.2.2 SpinTAC™ 速度移动运行函数
      3. 3.6.3 SpinTAC™ 速度规划
        1. 3.6.3.1 SpinTAC™ 速度规划接口
        2. 3.6.3.2 SpinTAC™ 速度规划主函数
      4. 3.6.4 SpinTAC™ 速度识别
        1. 3.6.4.1 SpinTAC™ 速度识别接口
        2. 3.6.4.2 SpinTAC™ 速度识别运行函数
      5. 3.6.5 SpinTAC™ 位置转换
        1. 3.6.5.1 SpinTAC™ 位置转换接口
        2. 3.6.5.2 SpinTAC™ 位置转换运行函数
      6. 3.6.6 SpinTAC™ 位置控制
        1. 3.6.6.1 SpinTAC™ 位置控制接口
        2. 3.6.6.2 SpinTAC™ 位置控制运行函数
      7. 3.6.7 SpinTAC™ 位置移动
        1. 3.6.7.1 SpinTAC™ 位置移动接口
        2. 3.6.7.2 SpinTAC™ 位置移动运行函数
      8. 3.6.8 SpinTAC™ 位置规划
        1. 3.6.8.1 SpinTAC™ 位置规划接口
        2. 3.6.8.2 SpinTAC 位置规划主函数
      9. 3.6.9 SpinTAC™ 函数
  5. 4 用户参数 (user.h)
    1. 4.1 电流和电压
      1. 4.1.1  USER_IQ_FULL_SCALE_FREQ_Hz
      2. 4.1.2  USER_IQ_FULL_SCALE_VOLTAGE_V
      3. 4.1.3  USER_ADC_FULL_SCALE_VOLTAGE_V
      4. 4.1.4  USER_VOLTAGE_SF
      5. 4.1.5  USER_IQ_FULL_SCALE_CURRENT_A
      6. 4.1.6  USER_ADC_FULL_SCALE_CURRENT_A
      7. 4.1.7  USER_CURRENT_SF
      8. 4.1.8  USER_NUM_CURRENT_SENSORS
      9. 4.1.9  USER_NUM_VOLTAGE_SENSORS
      10. 4.1.10 I_A_offset、I_B_offset、I_C_offset
      11. 4.1.11 V_A_offset、V_B_offset、V_C_offset
    2. 4.2 时钟与定时器
      1. 4.2.1 USER_SYSTEM_FREQ_MHz
      2. 4.2.2 USER_PWM_FREQ_kHz
      3. 4.2.3 USER_MAX_VS_MAG_PU
      4. 4.2.4 USER_PWM_PERIOD_usec
      5. 4.2.5 USER_ISR_FREQ_Hz
      6. 4.2.6 USER_ISR_PERIOD_usec
    3. 4.3 抽取率
      1. 4.3.1  USER_NUM_PWM_TICKS_PER_ISR_TICK
      2. 4.3.2  USER_NUM_ISR_TICKS_PER_CTRL_TICK
      3. 4.3.3  USER_NUM_CTRL_TICKS_PER_CURRENT_TICK
      4. 4.3.4  USER_NUM_CTRL_TICKS_PER_EST_TICK
      5. 4.3.5  USER_NUM_CTRL_TICKS_PER_SPEED_TICK
      6. 4.3.6  USER_NUM_CTRL_TICKS_PER_TRAJ_TICK
      7. 4.3.7  USER_CTRL_FREQ_Hz
      8. 4.3.8  USER_EST_FREQ_Hz
      9. 4.3.9  USER_TRAJ_FREQ_Hz
      10. 4.3.10 USER_CTRL_PERIOD_usec
      11. 4.3.11 USER_CTRL_PERIOD_sec
    4. 4.4 限制
      1. 4.4.1  USER_MAX_NEGATIVE_ID_REF_CURRENT_A
      2. 4.4.2  USER_ZEROSPEEDLIMIT
      3. 4.4.3  USER_FORCE_ANGLE_FREQ_Hz
      4. 4.4.4  USER_MAX_CURRENT_SLOPE_POWERWARP
      5. 4.4.5  USER_MAX_ACCEL_Hzps
      6. 4.4.6  USER_MAX_ACCEL_EST_Hzps
      7. 4.4.7  USER_MAX_CURRENT_SLOPE
      8. 4.4.8  USER_IDRATED_FRACTION_FOR_RATED_FLUX
      9. 4.4.9  USER_IDRATED_FRACTION_FOR_L_IDENT
      10. 4.4.10 USER_IDRATED_DELTA
      11. 4.4.11 USER_SPEEDMAX_FRACTION_FOR_L_IDENT
      12. 4.4.12 USER_FLUX_FRACTION
      13. 4.4.13 USER_POWERWARP_GAIN
      14. 4.4.14 USER_R_OVER_L_EST_FREQ_Hz
    5. 4.5 极
      1. 4.5.1 USER_VOLTAGE_FILTER_POLE_Hz
      2. 4.5.2 USER_VOLTAGE_FILTER_POLE_rps
      3. 4.5.3 USER_OFFSET_POLE_rps
      4. 4.5.4 USER_FLUX_POLE_rps
      5. 4.5.5 USER_DIRECTION_POLE_rps
      6. 4.5.6 USER_SPEED_POLE_rps
      7. 4.5.7 USER_DCBUS_POLE_rps
      8. 4.5.8 USER_EST_KAPPAQ
    6. 4.6 使用电机和识别设置
      1. 4.6.1  USER_MOTOR_TYPE
      2. 4.6.2  USER_MOTOR_NUM_POLE_PAIRS
      3. 4.6.3  USER_MOTOR_Rr
      4. 4.6.4  USER_MOTOR_Rs
      5. 4.6.5  USER_MOTOR_Ls_d
      6. 4.6.6  USER_MOTOR_Ls_q
      7. 4.6.7  USER_MOTOR_RATED_FLUX
      8. 4.6.8  USER_MOTOR_MAGNETIZING_CURRENT
      9. 4.6.9  USER_MOTOR_RES_EST_CURRENT
      10. 4.6.10 USER_MOTOR_IND_EST_CURRENT
      11. 4.6.11 USER_MOTOR_MAX_CURRENT
      12. 4.6.12 USER_MOTOR_FLUX_EST_FREQ_Hz
      13. 4.6.13 USER_MOTOR_ENCODER_LINES（仅限 InstaSPIN-MOTION™）
      14. 4.6.14 USER_MOTOR_MAX_SPEED_KRPM（仅限 InstaSPIN-MOTION™）
      15. 4.6.15 USER_SYSTEM_INERTIA（仅限 InstaSPIN-MOTION™）
      16. 4.6.16 USER_SYSTEM_FRICTION（仅限 InstaSPIN-MOTION）
      17. 4.6.17 USER_SYSTEM_BANDWIDTH_SCALE（仅限 InstaSPIN-MOTION™）
    7. 4.7 SpinTAC™ 参数（spintac_velocity.h 和 spintac_position.h）
      1. 4.7.1 宏定义
        1. 4.7.1.1  ST_MREV_ROLLOVER（仅限 spintac_position.h）
        2. 4.7.1.2  ST_EREV_MAXIMUM（仅限 spintac_position.h）
        3. 4.7.1.3  ST_POS_ERROR_MAXIMUM_MREV（仅限 spintac_position.h）
        4. 4.7.1.4  ST_ISR_TICKS_PER_SPINTAC_TICK
        5. 4.7.1.5  ST_SPEED_SAMPLE_TIME
        6. 4.7.1.6  ST_SPEED_PU_PER_KRPM
        7. 4.7.1.7  ST_SPEED_KRPM_PER_PU
        8. 4.7.1.8  ST_MOTOR_INERTIA_PU
        9. 4.7.1.9  ST_MOTOR_FRICTION_PU
        10. 4.7.1.10 ST_MIN_ID_SPEED_RPM
        11. 4.7.1.11 ST_MIN_ID_SPEED_PU
        12. 4.7.1.12 ST_ID_INCOMPLETE_ERROR
        13. 4.7.1.13 ST_VARS_DEFAULTS
      2. 4.7.2 类型定义
        1. 4.7.2.1 VEL_Params_t/POS_Params_t
        2. 4.7.2.2 ST_Obj
        3. 4.7.2.3 ST_Handle
        4. 4.7.2.4 ST_PlanButton_e
        5. 4.7.2.5 ST_Vars_t
      3. 4.7.3 函数
        1. 4.7.3.1  ST_init
        2. 4.7.3.2  ST_setupPosConv
        3. 4.7.3.3  ST_setupVelCtl（仅限速度控制）
        4. 4.7.3.4  ST_setupPosCtl（仅限位置控制）
        5. 4.7.3.5  ST_setupVelMove（仅限速度控制）
        6. 4.7.3.6  ST_setupPosMove（仅限位置控制）
        7. 4.7.3.7  ST_setupVelPlan（仅限速度控制）
        8. 4.7.3.8  ST_setupPosPlan（仅限位置控制）
        9. 4.7.3.9  ST_setupVelId（仅限速度控制）
        10. 4.7.3.10 ST_runPosConv
        11. 4.7.3.11 ST_runVelCtl（仅限速度控制）
        12. 4.7.3.12 ST_runPosCtl（仅限位置控制）
        13. 4.7.3.13 ST_runVelMove（仅限速度控制）
        14. 4.7.3.14 ST_runPosMove（仅限位置控制）
        15. 4.7.3.15 ST_runVelPlan（仅限速度控制）
        16. 4.7.3.16 ST_runVelPlanTick（仅限速度控制）
        17. 4.7.3.17 ST_runPosPlan（仅限位置控制）
        18. 4.7.3.18 ST_runPosPlanTick（仅限位置控制）
        19. 4.7.3.19 ST_runVelId（仅限速度控制）
    8. 4.8 在 user.h 中设置 ACIM 电机参数
      1. 4.8.1 从 ACIM 数据表中获取这些参数
        1. 4.8.1.1 极对数
        2. 4.8.1.2 将数据表中的 ACIM 电机参数输入 user.h 中
        3. 4.8.1.3 获取 ACIM 的额定磁化电流
        4. 4.8.1.4 获取 ACIM 的额定磁通
  6. 5 管理电机信号
    1. 5.1 软件必要条件
      1. 5.1.1 IQ 满量程频率
      2. 5.1.2 IQ 满量程电压
      3. 5.1.3 IQ 满量程电流
      4. 5.1.4 最大电流
      5. 5.1.5 抽取率
      6. 5.1.6 系统频率
      7. 5.1.7 PWM 频率
      8. 5.1.8 最大电压矢量
    2. 5.2 硬件必要条件
      1. 5.2.1 电流反馈增益
      2. 5.2.2 电流反馈极性
        1. 5.2.2.1 正反馈
        2. 5.2.2.2 负反馈
      3. 5.2.3 电压反馈
      4. 5.2.4 电压滤波器极点
      5. 5.2.5 分流电阻器数量
      6. 5.2.6 死区时间配置
      7. 5.2.7 模拟输入配置
      8. 5.2.8 PWM 输出配置
  7. 6 电机识别和状态图
    1. 6.1  概述
    2. 6.2  InstaSPIN™ 电机识别
    3. 6.3  电机识别过程概述
      1. 6.3.1 控制器 (CTRL) 状态机
      2. 6.3.2 估算器 (EST) 状态机
      3. 6.3.3 控制器 (CTRL) 和估算器 (EST) 状态机的相关性
    4. 6.4  PMSM 和 ACIM 识别过程的差别
    5. 6.5  必要条件
      1. 6.5.1 机械必要条件
        1. 6.5.1.1 电机连接
        2. 6.5.1.2 相序
        3. 6.5.1.3 最小机械负载
      2. 6.5.2 硬件必要条件
      3. 6.5.3 软件必要条件
      4. 6.5.4 PMSM 电机识别的软件配置
        1. 6.5.4.1 电机类型
        2. 6.5.4.2 极对数
        3. 6.5.4.3 Rhf 和 Lhf 频率
        4. 6.5.4.4 Rs 电流
        5. 6.5.4.5 Ls 电流
        6. 6.5.4.6 Ls 和磁通频率
      5. 6.5.5 ACIM 电机识别的软件配置
        1. 6.5.5.1 电机类型
        2. 6.5.5.2 极对数
        3. 6.5.5.3 Rhf 和 Lhf 频率
        4. 6.5.5.4 额定磁通
        5. 6.5.5.5 Rs 电流
        6. 6.5.5.6 IdRated、Ls 和 Rr 频率
    6. 6.6  PMSM 电机完全识别
      1. 6.6.1  CTRL_State_Idle 和 EST_State_Idle
      2. 6.6.2  CTRL_State_OffLine 和 EST_State_Idle（硬件偏移已校准）
      3. 6.6.3  CTRL_State_OnLine 和 EST_State_RoverL
        1. 6.6.3.1 RoverL 状态下注入电流的幅值
        2. 6.6.3.2 RoverL 状态下注入电流的频率
        3. 6.6.3.3 RoverL 状态下的测量时间
        4. 6.6.3.4 RoverL 识别期间的电流控制器稳定性故障排除
        5. 6.6.3.5 调节高速电机产生的电流控制器增益
      4. 6.6.4  CTRL_State_OnLine 和 EST_State_Rs
        1. 6.6.4.1 Rs 识别期间的电流控制器稳定性故障排除
      5. 6.6.5  CTRL_State_OnLine 和 EST_State_RampUp
        1. 6.6.5.1 斜升电流幅值
          1. 6.6.5.1.1 斜升期间的电机转轴停转故障排除
        2. 6.6.5.2 斜升时间和加速度
          1. 6.6.5.2.1 平滑斜坡的电机转轴故障排除
        3. 6.6.5.3 PMSM 最终斜升速度
      6. 6.6.6  CTRL_State_OnLine 和 EST_State_RatedFlux
        1. 6.6.6.1 电流斜降
        2. 6.6.6.2 总测量时间
        3. 6.6.6.3 磁通测量故障排除
      7. 6.6.7  CTRL_State_OnLine 和 EST_State_Ls
        1. 6.6.7.1 斜升电流
        2. 6.6.7.2 Ls 识别故障排除
        3. 6.6.7.3 Ls_d 和 Ls_q（定子直流电感和定子正交电感）
      8. 6.6.8  CTRL_State_OnLine 和 EST_State_RampDown
      9. 6.6.9  CTRL_State_OnLine 和 EST_State_MotorIdentified
      10. 6.6.10 CTRL_State_Idle 和 EST_State_Idle
    7. 6.7  ACIM 电机完全识别
      1. 6.7.1  CTRL_State_Idle 和 EST_State_Idle
      2. 6.7.2  CTRL_State_OffLine 和 EST_State_Idle
      3. 6.7.3  CTRL_State_OnLine 和 EST_State_RoverL
      4. 6.7.4  CTRL_State_OnLine 和 EST_State_Rs
      5. 6.7.5  CTRL_State_OnLine 和 EST_State_RampUp
        1. 6.7.5.1 ACIM 最终斜升速度
      6. 6.7.6  CTRL_State_OnLine 和 EST_State_IdRated
        1. 6.7.6.1 减少振荡以改善 Id 额定电流测量
        2. 6.7.6.2 读取 Id 额定电流最终值
      7. 6.7.7  CTRL_State_OnLine 和 EST_State_RatedFlux
        1. 6.7.7.1 磁通测量故障排除
      8. 6.7.8  CTRL_State_OnLine 和 EST_State_RampDown
      9. 6.7.9  CTRL_State_Idle 和 EST_State_LockRotor
        1. 6.7.9.1 锁定转子测试故障排除
      10. 6.7.10 CTRL_State_OnLine 和 EST_State_Ls
      11. 6.7.11 CTRL_State_OnLine 和 EST_State_Rr
      12. 6.7.12 CTRL_State_OnLine 和 EST_State_RampDown
      13. 6.7.13 CTRL_State_OnLine 和 EST_State_MotorIdentified
      14. 6.7.14 CTRL_State_Idle 和 EST_State_Idle
    8. 6.8  PMSM 和 ACIM 电机识别重校准
      1. 6.8.1 完全识别后的 PMSM 和 ACIM 电机重校准
        1. 6.8.1.1 启动阶段注意事项
        2. 6.8.1.2 CTRL_State_Idle 和 EST_State_Idle
        3. 6.8.1.3 CTRL_State_OffLine 和 EST_State_Idle
        4. 6.8.1.4 CTRL_State_OnLine 和 EST_State_Rs
          1. 6.8.1.4.1 管理 Rs 重校准所需的时间
          2. 6.8.1.4.2 Rs 重校准的软件配置
        5. 6.8.1.5 CTRL_State_OnLine 和 EST_State_OnLine
          1. 6.8.1.5.1 从 CTRL 在线状态和 EST Rs 状态转换到在线状态
          2. 6.8.1.5.2 从（CTRL 空闲状态或 CTRL 离线状态）和 EST 空闲状态转换到在线状态
        6. 6.8.1.6 CTRL_State_Idle 和 EST_State_Idle
      2. 6.8.2 使用 user.h 中的参数后的 PMSM 和 ACIM 电机重校准
    9. 6.9  在 user.h 中设置 PMSM 电机参数
      1. 6.9.1 从 PMSM 数据表中获取参数
        1. 6.9.1.1 极对数
        2. 6.9.1.2 定子电阻 (Rs)
        3. 6.9.1.3 定子电感（Ls_d 和 Ls_q）
        4. 6.9.1.4 额定磁通 (ψ)
    10. 6.10 电机识别故障排除
      1. 6.10.1 PMSM 电机识别故障排除
        1. 6.10.1.1 在负载无法断开时识别 PMSM 电机
        2. 6.10.1.2 电机能否在连接负载的情况下旋转？
        3. 6.10.1.3 运行电机识别的前三个步骤
        4. 6.10.1.4 通过 user.h 中的电机参数运行
        5. 6.10.1.5 斜升期间的电机转轴停转故障排除
        6. 6.10.1.6 平滑斜坡的电机转轴故障排除
        7. 6.10.1.7 磁通测量故障排除
        8. 6.10.1.8 Ls 识别故障排除
          1. 6.10.1.8.1 识别低电感 PMSM 电机
            1. 6.10.1.8.1.1 硬件注意事项
            2. 6.10.1.8.1.2 软件注意事项
          2. 6.10.1.8.2 识别凸极 PMSM 电机的电感
            1. 6.10.1.8.2.1 硬件注意事项
            2. 6.10.1.8.2.2 软件注意事项
        9. 6.10.1.9 识别高齿槽转矩 PMSM 电机
      2. 6.10.2 ACIM 电机识别故障排除
        1. 6.10.2.1 磁通测量故障排除
        2. 6.10.2.2 锁定转子测试故障排除
  8. 7 惯性识别
    1. 7.1 概述
    2. 7.2 InstaSPIN-MOTION™ 惯性识别
    3. 7.3 惯性识别过程概述
    4. 7.4 SpinTAC™ 速度识别的软件配置
      1. 7.4.1 包括头文件
      2. 7.4.2 声明全局变量
      3. 7.4.3 初始化配置变量
      4. 7.4.4 调用 SpinTAC™ 速度识别
    5. 7.5 惯性识别故障排除
      1. 7.5.1 ERR_ID
      2. 7.5.2 2003 错误
      3. 7.5.3 2004 错误
        1. 7.5.3.1 电机持续转动
        2. 7.5.3.2 电机初始未转动
      4. 7.5.4 2006 错误
    6. 7.6 不易识别惯性的应用
      1. 7.6.1 自动泵（齿槽力大/摩擦力大）
      2. 7.6.2 直接驱动型洗衣机（额定转速低且反电势大）
      3. 7.6.3 压缩机（启动电流大）
  9. 8 MCU 注意事项
    1. 8.1 概述
    2. 8.2 支持 InstaSPIN 的器件
      1. 8.2.1 softwareUpdate1p6() - 用户代码中所需的函数
    3. 8.3 ROM 和用户内存概述
      1. 8.3.1 ROM 中的 InstaSPIN-FOC™ 完全执行
        1. 8.3.1.1 从 ROM 和 RAM 中执行
        2. 8.3.1.2 从 ROM 和闪存中执行
      2. 8.3.2 ROM 中的 InstaSPIN-FOC™ 最小实现
        1. 8.3.2.1 从 ROM 和 RAM 中执行
        2. 8.3.2.2 从 ROM 和闪存中执行
      3. 8.3.3 ROM 中的 InstaSPIN-MOTION™
        1. 8.3.3.1 在主中断内执行 InstaSPIN™-MOTION
        2. 8.3.3.2 从 RAM 中执行库
        3. 8.3.3.3 从闪存中执行库
    4. 8.4 关于 CPU 负载和内存占用量测量的详细信息
      1. 8.4.1 CPU 利用率测量详情
      2. 8.4.2 内存分配测量详情
      3. 8.4.3 在 ROM 中构建 IQmath
      4. 8.4.4 堆栈利用率测量详情
      5. 8.4.5 InstaSPIN™ 主中断
      6. 8.4.6 时钟速率
    5. 8.5 内存占用量
      1. 8.5.1 器件内存映射
        1. 8.5.1.1 F2806xF 和 F2806xM 器件
        2. 8.5.1.2 F2805xF 和 F2805xM 器件
        3. 8.5.1.3 F2802xF 器件
      2. 8.5.2 InstaSPIN™ 内存占用量
        1. 8.5.2.1 F2806xF 和 F2805xF 器件
        2. 8.5.2.2 F2802xF 器件
        3. 8.5.2.3 F2806xM 和 F2805xM 器件
      3. 8.5.3 内存等待状态
        1. 8.5.3.1 F2806xF/M 器件
        2. 8.5.3.2 F2805xF/M 器件
        3. 8.5.3.3 F2802xF 器件
      4. 8.5.4 用于仅 RAM 执行的所需闪存配置
      5. 8.5.5 只执行内存的调试 (IDE)
    6. 8.6 CPU 负载
      1. 8.6.1 F2806xF 器件
        1. 8.6.1.1 CPU 周期数
          1. 8.6.1.1.1 RAM 中的用户代码
            1. 8.6.1.1.1.1 完全执行
            2. 8.6.1.1.1.2 最小执行
          2. 8.6.1.1.2 闪存中的用户代码
            1. 8.6.1.1.2.1 完全执行
            2. 8.6.1.1.2.2 最小执行
        2. 8.6.1.2 PWM = 10kHz 时的 CPU 负载
        3. 8.6.1.3 PWM = 20kHz 时的 CPU 负载
        4. 8.6.1.4 CPU 负载示例
          1. 8.6.1.4.1 F2806xF 器件示例 1
          2. 8.6.1.4.2 F2806xF 器件示例 2
      2. 8.6.2 F2806xM 器件
        1. 8.6.2.1 CPU 周期数
          1. 8.6.2.1.1 RAM 执行 - SpinTAC™ 库和用户代码
          2. 8.6.2.1.2 闪存执行 - SpinTAC™ 库和用户代码
        2. 8.6.2.2 CPU 负载示例
          1. 8.6.2.2.1 F2806xM 器件示例 1
          2. 8.6.2.2.2 F2806xM 器件示例 2
          3. 8.6.2.2.3 F2806xM 器件示例 3
          4. 8.6.2.2.4 F2806xM 器件示例 4（SpinTAC™ 位置）
      3. 8.6.3 F805xF 器件
        1. 8.6.3.1 CPU 周期数
        2. 8.6.3.2 PWM = 10kHz 时的 CPU 负载
        3. 8.6.3.3 PWM = 20kHz 时的 CPU 负载
      4. 8.6.4 F2805xM 器件
        1. 8.6.4.1 CPU 周期数
          1. 8.6.4.1.1 闪存执行 - SpinTAC™ 库和用户代码
      5. 8.6.5 F2802xF 器件
        1. 8.6.5.1 CPU 周期数
        2. 8.6.5.2 PWM = 10kHz 时的 CPU 负载
        3. 8.6.5.3 PWM = 20kHz 时的 CPU 负载
    7. 8.7 数字和模拟引脚
      1. 8.7.1 引脚利用率
      2. 8.7.2 F2805x 模拟前端 (AFE)
        1. 8.7.2.1 AFE 模块注意事项
        2. 8.7.2.2 电流信号传输
        3. 8.7.2.3 基准电压连接
        4. 8.7.2.4 电压信号传输
  10. 9 实时结构
    1. 9.1 InstaSPIN™ 软件执行时钟树
    2. 9.2 用于实时调度的软件抽取
      1. 9.2.1 USER_NUM_ISR_TICKS_PER_CTRL_TICK
      2. 9.2.2 USER_NUM_CTRL_TICKS_PER_CURRENT_TICK
      3. 9.2.3 USER_NUM_CTRL_TICKS_PER_EST_TICK
      4. 9.2.4 实例
      5. 9.2.5 USER_NUM_CTRL_TICKS_PER_SPEED_TICK
      6. 9.2.6 USER_NUM_CTRL_TICKS_PER_TRAJ_TICK
    3. 9.3 硬件抽取
  11. 10管理启动时间
    1. 10.1 同时启用偏移和 Rs 重校准功能的启动
    2. 10.2 仅启用偏移重校准时的启动
    3. 10.3 启用 Rs 重校准时的启动
    4. 10.4 不启用任何重校准时的启动
    5. 10.5 忽略惯性估算
  12. 11调整稳压器
    1. 11.1 PI 控制器简介
    2. 11.2 电流控制器的 PI 设计
    3. 11.3 速度控制器的 PI 设计
    4. 11.4 根据稳定性和带宽计算 PI 增益
    5. 11.5 根据阻尼因子计算速度和电流 PI 增益
    6. 11.6 向速度环路添加极点时的考量
    7. 11.7 速度 PI 控制器注意事项：电流限制、钳位和惯性
    8. 11.8 为 FOC 系统设计 PI 控制器时的注意事项
      1. 11.8.1 电机类型间的 FOC 差异
      2. 11.8.2 Q 轴与 D 轴间的耦合
    9. 11.9 采样和数字系统考量
      1. 11.9.1 积分增益中的采样周期考量
      2. 11.9.2 数字格式考量
      3. 11.9.3 PI 系数换算考量
  13. 12InstaSPIN-MOTION™ 控制器
    1. 12.1 概述
    2. 12.2 稳定性
      1. 12.2.1 稳定性量化分析
        1. 12.2.1.1 SpinTAC™ 速度控制稳定性
        2. 12.2.1.2 SpinTAC™ 位置控制稳定性
      2. 12.2.2 性能
        1. 12.2.2.1 频域分析
        2. 12.2.2.2 时域分析
      3. 12.2.3 稳定性和性能之间的权衡
      4. 12.2.4 调整 SpinTAC™ 控制器
        1. 12.2.4.1 注意事项
        2. 12.2.4.2 调整 InstaSPIN™-MOTION 控制器
    3. 12.3 SpinTAC™ 速度控制的软件配置
      1. 12.3.1 包括头文件
      2. 12.3.2 声明全局结构
      3. 12.3.3 初始化配置变量
      4. 12.3.4 调用 SpinTAC™ 速度控制
      5. 12.3.5 SpinTAC™ 速度控制故障排除
        1. 12.3.5.1 ERR_ID
    4. 12.4 速度控制中的最优性能
      1. 12.4.1 简介
      2. 12.4.2 比较速度控制器
      3. 12.4.3 抗扰
      4. 12.4.4 系统配置跟踪
      5. 12.4.5 InstaSPIN-MOTION™ 速度控制优势
        1. 12.4.5.1 单个参数调整
        2. 12.4.5.2 抗扰测试
        3. 12.4.5.3 前馈
        4. 12.4.5.4 无积分器饱和
        5. 12.4.5.5 最小启动过冲
        6. 12.4.5.6 结论
    5. 12.5 SpinTAC™ 位置控制的软件配置
      1. 12.5.1 包括头文件
      2. 12.5.2 声明全局结构
      3. 12.5.3 初始化配置变量
      4. 12.5.4 调用 SpinTAC™ 位置控制
      5. 12.5.5 SpinTAC™ 位置控制故障排除
        1. 12.5.5.1 ERR_ID
    6. 12.6 位置控制中的出色性能
      1. 12.6.1 简介
      2. 12.6.2 比较位置控制器
      3. 12.6.3 抗扰
      4. 12.6.4 系统配置跟踪
      5. 12.6.5 InstaSPIN-MOTION™ 位置控制优势
        1. 12.6.5.1 单个参数调整
        2. 12.6.5.2 抗扰
        3. 12.6.5.3 前馈
        4. 12.6.5.4 低速运行和平滑启动
        5. 12.6.5.5 最小阶跃响应稳定时间
        6. 12.6.5.6 结论
  14. 13轨迹规划
    1. 13.1 生成 InstaSPIN-MOTION™ 系统配置
      1. 13.1.1 急动对系统性能的影响
    2. 13.2 SpinTAC™ 速度移动的软件配置
      1. 13.2.1 包括头文件
      2. 13.2.2 声明全局结构
      3. 13.2.3 初始化配置变量
      4. 13.2.4 调用 SpinTAC™ 速度移动
      5. 13.2.5 SpinTAC™ 速度移动故障排除
        1. 13.2.5.1 ERR_ID
    3. 13.3 SpinTAC™ 位置移动的软件配置
      1. 13.3.1 包括头文件
      2. 13.3.2 声明全局结构
      3. 13.3.3 初始化配置变量
      4. 13.3.4 调用 SpinTAC™ 位置移动
      5. 13.3.5 SpinTAC™ 位置移动疑难解答
        1. 13.3.5.1 位置系统配置限制
        2. 13.3.5.2 ERR_ID
    4. 13.4 InstaSPIN-MOTION™ 序列计划
      1. 13.4.1 SpinTAC™ 速度规划元素
        1. 13.4.1.1 状态
        2. 13.4.1.2 转换
        3. 13.4.1.3 工作条件
        4. 13.4.1.4 变量
        5. 13.4.1.5 操作
      2. 13.4.2 SpinTAC™ 速度规划元素限制
        1. 13.4.2.1 确定 SpinTAC™ 速度规划配置数组大小的示例
      3. 13.4.3 SpinTAC™ 速度规划示例：洗衣机搅动
      4. 13.4.4 SpinTAC™ 速度规划示例：车库门
      5. 13.4.5 SpinTAC™ 速度规划示例：洗衣机
      6. 13.4.6 SpinTAC™ 位置规划示例：售货机
    5. 13.5 SpinTAC™ 速度规划的软件配置
      1. 13.5.1 包括头文件
      2. 13.5.2 定义配置数组的大小
      3. 13.5.3 声明全局结构
      4. 13.5.4 初始化配置变量
      5. 13.5.5 调用 SpinTAC™ 速度规划
      6. 13.5.6 调用 SpinTAC™ 速度规划节拍
      7. 13.5.7 根据 SpinTAC™ 速度移动状态更新 SpinTAC™ 速度规划
    6. 13.6 SpinTAC™ 速度规划疑难解答
      1. 13.6.1 ERR_ID
      2. 13.6.2 配置错误
    7. 13.7 SpinTAC™ 位置规划的软件配置
      1. 13.7.1 包括头文件
      2. 13.7.2 定义配置数组的大小
      3. 13.7.3 声明全局结构
      4. 13.7.4 初始化配置变量
      5. 13.7.5 调用 SpinTAC™ 位置规划
      6. 13.7.6 调用 SpinTAC™ 位置规划节拍
      7. 13.7.7 根据 SpinTAC™ 位置移动状态更新 SpinTAC™ 位置规划
    8. 13.8 SpinTAC™ 位置计划故障排除
      1. 13.8.1 ERR_ID
      2. 13.8.2 配置错误
    9. 13.9 结论
  15. 14管理启动、低速和换向时的满负载
    1. 14.1 概述
    2. 14.2 满载低速运行
      1. 14.2.1 满载低速运行时的考量
        1. 14.2.1.1 启用偏移重校准
        2. 14.2.1.2 启用定子 Rs 重校准
        3. 14.2.1.3 禁用强制角
        4. 14.2.1.4 调整速度控制器以避免电机停转
        5. 14.2.1.5 调整电压反馈电路
      2. 14.2.2 瞬时满载低速运行示例
        1. 14.2.2.1 4Hz，无负载至满载瞬态
        2. 14.2.2.2 2Hz，无负载至满载瞬态
    3. 14.3 满载换向
      1. 14.3.1 满载低速运行时的换向考量
      2. 14.3.2 满载低速运行时的换向示例
        1. 14.3.2.1 满载情况下从 -4 至 +4Hz
        2. 14.3.2.2 满载情况下从 -2 至 +2 Hz
    4. 14.4 满载电机启动
      1. 14.4.1 满载电机启动的考量
        1. 14.4.1.1 启用强制角
      2. 14.4.2 满载电机启动示例
        1. 14.4.2.1 满载情况下从静止至 4Hz
        2. 14.4.2.2 满载情况下从静止至 2Hz
    5. 14.5 满载从静止状态快速加速
      1. 14.5.1 无需电机对准时满载最快速度启动电机的考量
        1. 14.5.1.1 加载有效偏移并禁用偏移重校准
        2. 14.5.1.2 加载有效 Rs 并禁用 Rs 重校准
        3. 14.5.1.3 无需电机对准时满载最快速度启动电机的示例
      2. 14.5.2 需要电机对准时满载最快速度启动电机的考量
        1. 14.5.2.1 最大化电流斜率
        2. 14.5.2.2 需要电机对准时满载最快速度启动电机的示例
    6. 14.6 过载和电机过热
      1. 14.6.1 过载和电机过热的考量
      2. 14.6.2 过载和电机过热示例
    7. 14.7 InstaSPIN-MOTION™ 和低速运行的考量
  16. 15Rs 在线重校准
    1. 15.1  概要
    2. 15.2  电阻与温度之间的关系
    3. 15.3  低速运行（包括启动）时所需的 Rs 准确值
    4. 15.4  Rs 在线重校准介绍
    5. 15.5  Rs 在线重校准与 Rs 离线重校准
    6. 15.6  启用 Rs 在线重校准
    7. 15.7  禁用 Rs 在线重校准
    8. 15.8  修改 Rs 在线参数
      1. 15.8.1 调整注入电流幅度
      2. 15.8.2 调整慢速转角
      3. 15.8.3 调整 Rs 在线值递增和递减的增量
      4. 15.8.4 调整滤波器参数
    9. 15.9  监控 Rs 在线电阻值
      1. 15.9.1 Rs 在线浮点值
      2. 15.9.2 Rs 在线定点值
    10. 15.10 使用 Rs 在线特性作为温度传感器
    11. 15.11 Rs 在线特性相关状态框图（CTRL 和 EST）
  17. 16PowerWarp™
    1. 16.1 概述
    2. 16.2 启用 PowerWarp™ 软件
    3. 16.3 PowerWarp™ 电流斜率
    4. 16.4 实例
    5. 16.5 案例研究
  18. 17分流电流测量
    1. 17.1 简介
    2. 17.2 信号
    3. 17.3 1 分流
    4. 17.4 2 分流
    5. 17.5 3 分流
    6. 17.6 开发套件
      1. 17.6.1 DRV8312 套件
      2. 17.6.2 DRV8301 套件
    7. 17.7 结论
  19. 18传感系统
    1. 18.1 正交编码器的硬件配置
      1. 18.1.1 引脚用量
    2. 18.2 正交编码器的软件配置
      1. 18.2.1 针对 EQEP 操作配置电机
      2. 18.2.2 初始化 EQEP 句柄
      3. 18.2.3 设置数字 IO 以连接 QEP 外设
      4. 18.2.4 启用 eQEP 时钟
      5. 18.2.5 初始化 ENC 模块
      6. 18.2.6 设置 ENC 模块
      7. 18.2.7 调用 eQEP 函数
      8. 18.2.8 为 FOC 提供 eQEP 角度
    3. 18.3 InstaSPIN-MOTION™ 位置转换
      1. 18.3.1 SpinTAC™ 位置转换的软件配置
        1. 18.3.1.1 包括头文件
        2. 18.3.1.2 声明全局结构
        3. 18.3.1.3 初始化配置变量
        4. 18.3.1.4 调用 SpinTAC™ 位置转换
      2. 18.3.2 SpinTAC™ 位置转换疑难解答
        1. 18.3.2.1 ERR_ID
  20.   A 术语和缩略词定义
  21.   B 修订历史记录

11.4 根据稳定性和带宽计算 PI 增益

在上一节结束时，我们讨论了使用单个参数帮助调整电机控制系统中的速度 PI 环路的可能性。要深入研究此参数，让我们回顾整个速度环路的开环传递函数：

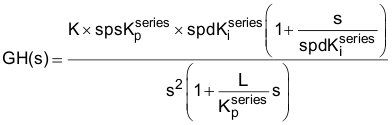
Equation49. GUID-95B49EF5-260E-44E0-B8A1-B12382F826A6-low.gif

其中：

  • K 是包含多个电机和负载相关项的系数
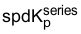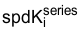  • GUID-897362A1-3A93-4F87-898D-5DF52367BEC8-low.gif 和 GUID-95B1FF69-058D-46E5-B16F-6D119A0F8EF8-low.gif 是速度环路的 PI 系数
  • L 是电机电感
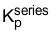  • GUID-6D5B57E6-F2FE-40D8-A092-23FD5C2554A6-low.gif 是电流环路的 PI 系数之一
  • s 是拉普拉斯频率变量

假设 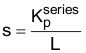GUID-228218A6-F505-4FEF-90E5-886A797B8AFB-low.gif 处极点的频率高于 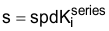GUID-6F9A799D-38C4-4936-AFC6-5B012A7FD88A-low.gif 处零点的频率，并且单位增益频率介于上述两个频率之间，则得到的波特图应与图 12-7 类似。

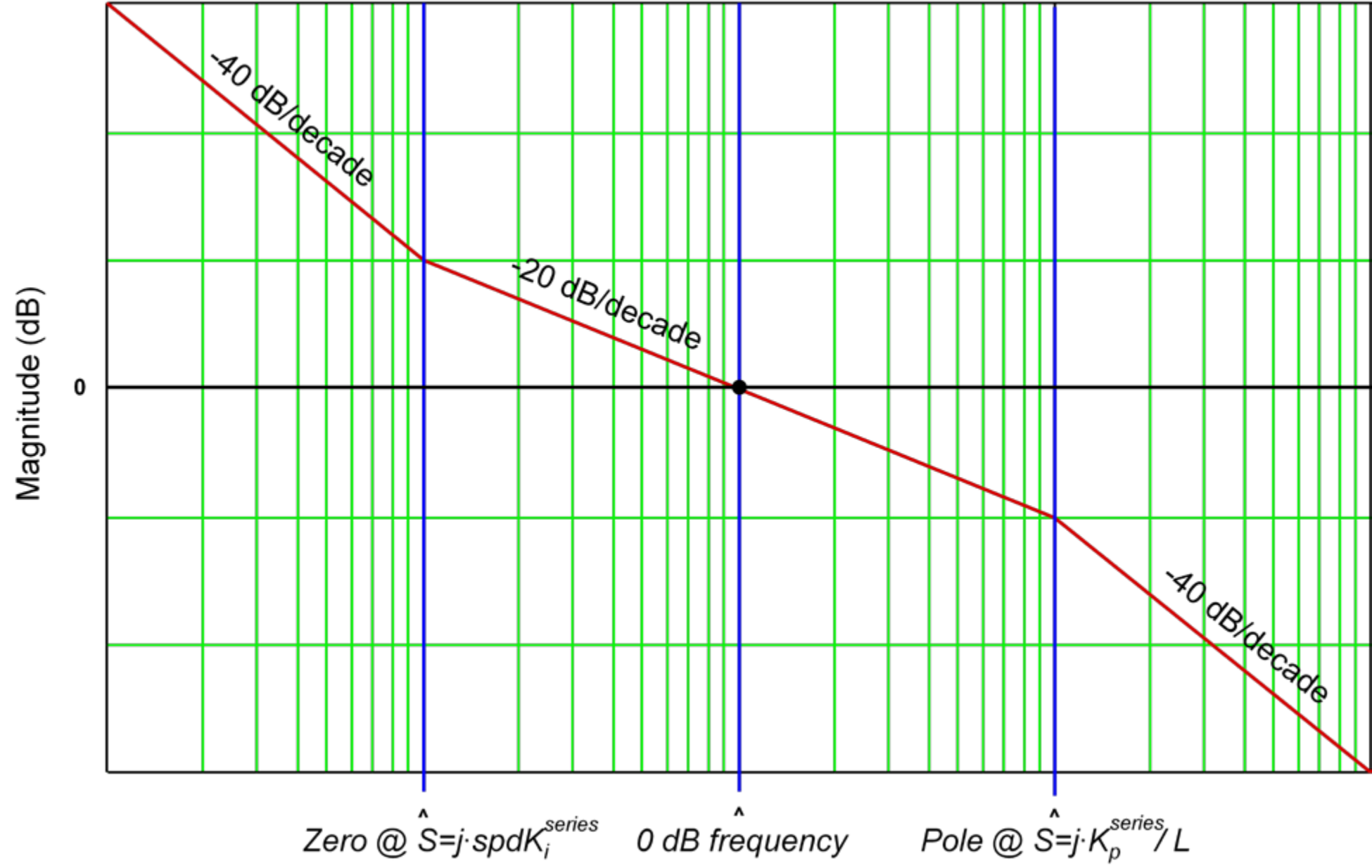GUID-73DB836D-3738-4981-A731-FFA6AC922754-low.png图 11-7 波特图

曲线形状之所以重要的原因是 0dB 频率处的相移决定着系统稳定性。在极点频率与零点频率之间分离已确定的情况下，为使相位裕度最大化（相移：180°），0dB 频率的位置应恰好在对数标度极点频率与零点频率之间的中点位置。即，

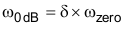
Equation50. GUID-4069C66C-0ECE-4AE9-BE8F-3E54EA868055-low.gif

和

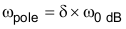
Equation51. GUID-0DEF52C7-4880-4618-8C17-88F23D403113-low.gif

将 Equation50 与 Equation51 合并可得到：

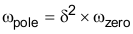
Equation52. GUID-578E5FF6-0092-46DD-9492-CE33ECD3291B-low.gif

通过Equation49，能够发现已在 PI 系数项中对 ω极点和 ω零点进行了定义。因此，

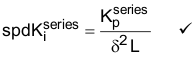
Equation53. GUID-4760A417-B88A-427E-B6D6-75CCEC63C61A-low.gif

其中，“δ”将定义为阻尼因子。δ 值越大，零点角频率与电流环路极点频率之间的分离程度越大。分离程度越大，两个频率之间所能够达到的相位裕度峰值越大。这种稳定性的提升建立在牺牲速度环路带宽的基础上。δ = 1 时，零点角频率与电流环路极点频率相等，这样能够消除极点/零点并且系统将变得不稳定。由于相位裕度 > 0，因此理论上只要 δ > 1 时，系统都是稳定的。但是，δ 的值接近 1 会导致性能上表现出严重的欠阻尼。

稍后会对 δ 进行详细介绍，我们现在将注意力转向最后一个系数的确定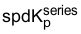：GUID-897362A1-3A93-4F87-898D-5DF52367BEC8-low.gif 。通过Equation50，我们发现速度环路的开环传递函数（Equation49）在频率等于零点拐点频率与 δ 的乘积时为单位增益 (0dB)。即，

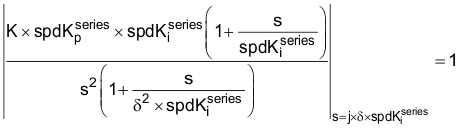
Equation54. GUID-FE314892-E394-4C67-874A-707A2744E4B5-low.gif

对Equation54 中的“s”进行指定替换和整理后，得到：

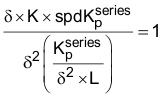
Equation55. GUID-7C4C1012-45CB-4370-A234-C2ABFC45F344-low.gif

最终可解出 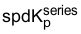GUID-897362A1-3A93-4F87-898D-5DF52367BEC8-low.gif：

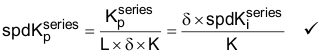
Equation56. GUID-9ED6213F-7E3B-441F-8572-1D5137213030-low.gif

现在我们来回顾一下整个过程。我们刚刚为含有两个独立 PI 控制器的电机（一个用于内部电流环路，另一个用于外部速度环路）设计了级联速度控制器。为了在电流环路中消除极点/零点，我们选择 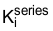GUID-1A1D7507-C3DF-454A-9DBC-CCDB2A345322-low.gif 为：

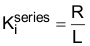
Equation57. GUID-7FC0D825-A57A-4E85-AA0C-226B167CA244-low.gif

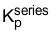GUID-6D5B57E6-F2FE-40D8-A092-23FD5C2554A6-low.gif 可设定电流控制器的带宽：

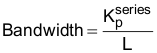
Equation58. GUID-91C383AA-C493-4C7E-8097-789487725B32-low.gif

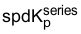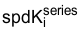定义了内部环路电流控制器参数后，接下来选择阻尼因子 (δ) 的值，该值能够精确量化速度环路稳定性和带宽之间的权衡。然后只需要对 GUID-897362A1-3A93-4F87-898D-5DF52367BEC8-low.gif 和 GUID-95B1FF69-058D-46E5-B16F-6D119A0F8EF8-low.gif 进行计算：

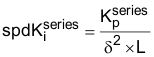
Equation59. GUID-16F5EFF9-83EC-41BA-BC6E-0660568532A0-low.gif
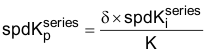
Equation60. GUID-92CC9D9D-5EE1-46C9-8236-54AFAF3F9B10-low.gif

这种方法不用根据经验调整四个看似与系统性能相关性很小的 PI 系数，而是只需要定义两个有意义的系统参数：电流控制器带宽和速度环路阻尼系数。完成上述选择后，将自动计算四个 PI 系数。

电流控制器带宽必须是有意义的系统参数，但在速度控制系统中我们通常先指定速度控制器的带宽，然后根据所指定的带宽值设置电流控制器带宽。在下一节中，我们进一步讨论阻尼因子并找到根据所需速度环路带宽设置电流环路带宽的方法。
千亿体育app官网登录(中国)官方网站IOS/安卓通用版/手机APP | 米乐app下载官网（中国）|ios|Android/通用版APP最新版 | 米乐|米乐·M6（中国大陆）官方网站 | 千亿体育登陆地址 | 华体会体育（中国）HTH·官方网站 | 千赢qy国际_全站最新版千赢qy国际V6.2.14安卓/IOS下载 | 18新利网v1.2.5|中国官方网站 | bob电竞真人（中国官网）安卓/ios苹果/电脑版【1.97.95版下载】 | 千亿体育app官方下载(中国)官方网站IOS/安卓/手机APP下载安装 |