过程

下一页的图 9 显示了用于计算立体视差的数据流程和计算链的概要框图。请注意，此处缺少图 6 所示 SFM 框图中存在的摄像机校准步骤，并且也不需要在密集立体视差算法中搜索特征。基于 SFM 的距离计算方法（根据物体的尺寸来计算距离）需要识别特征和物体。

图像秩变换通常是立体图像处理管道中的第一步或第二步。此步骤旨在确保两个图像之间的后续块比较在现实噪声情况（如左右图像之间的照度或亮度变化情况）下能够可靠完成 [7]。这些变化由许多因素引起。其中一些因素包括两个摄像机的视角各不相同而造成的照明度不同，以及快门速度之间的细微差异和其他抖动瑕疵，这些情况会导致摄像机在稍微不同的时间点捕获左右图像。

图 9 基于立体视差的距离计算的概要数据和算法流程。

如需了解图像的不同秩变换选项，以及这些选项如何影响视差计算的可靠性，可参考研究人员推荐的不同论文和方法 [8]。图 9 中的图像校正步骤确保了能够沿水平对极搜索线执行后续视差计算。该过程的后续步骤是视差的实际计算、计算的置信度以及后处理。尽管有一些方法提出在频域中计算视差，但密集视差计算主要在空域中进行 [9]。

这些方法试图利用大型 FFT 计算速度相对较快的优点，但是 FFT 还涉及其他复杂问题，因此整体上缺点更明显。本文无需深入进行这方面的讨论，可以肯定地说，大多数（即使不是全部）米6体育平台手机版_好二三四化的立体视差算法是在空域中实现的。在最基本的层面上，此分析要求，对于左侧（变换后）的图像中的每个像素，我们都需要选择它周围的一小块像素。

接下来，我们需要在右侧（变换后）的图像中沿着对极（水平）线搜索，直至找到同一块像素的位置。对于所有可能的视差值（从 1 到最大值，即 64 或 128 或者任何其他值），都会执行此计算。

左侧和右侧像素块之间的差异（或相关系数）将接近极小值（极大值），此值接近于像素视差的实际值。执行的“移动窗口”像素块比较和匹配过程将计算像素块已移动了多少，该结果将用于计算这个特定像素在 3D 空间中的距离。此过程如图 10 所示。在参考资料 [8] 中提供了这样一个示例，其中说明了使用秩变换的视差计算，然后是基于绝对差之和 (SAD) 的成本函数的最小化。

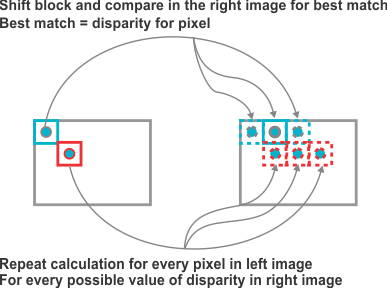图 10 用于发现视差的简单块比较算法，其基于 SAD 。

这种用于发现视差的基于 SAD 的方法非常巧妙，有时甚至过于简单。这种方法的基本前提是，对于给定的像素块，视差是相等的，但在物体的边缘几乎绝不会如此。如果再次查看图 2 并注意针对摩托车前叉和红色箱子所做的注释，您将很快意识到，许多相邻像素之间的视差会有所不同。这一点其实很正常，因为“储物架上的红色箱子”比起“前叉”离摄像机远约两米。一个小像素块的视差可能会在物体边界处发生剧烈变化，而对于倾斜或弯曲的表面则可能只发生轻微变化。Middlebury 数据集 [10] 中的“圆锥和面孔”图像充分突出了这一事实。在一个圆锥体（略微倾斜的表面）上找到的相邻像素将具有较小的视差变化，而物体边界将具有较大的视差差异。将基于 SAD 的简单算法与秩变换一起使用，这会在两个遮挡物上留下较大的视差孔洞，例如仅在一个摄像机和物体边界中可见的瑕疵。

为了根据确定的运行时间解决这种错误，[12] 中提出了一种巧妙的方法。

这种方法被称为“半全局匹配”法。在这种方法中会针对多个方向（4、8 或 16 个）上的每个像素计算平滑度成本函数。下方的图 11 展示了该成本函数的计算方式。其目的是针对每个像素在多个方向上优化成本函数 S(p,d)，并确保得到平滑的视差图。SGM 的原始论文推荐了优化成本函数的 16 个方向，但也尝试了 2、4 和 8 个方向的切实可行的实现方式。

图 11 SGM 优化成本函数方程式。

下一页的图 13 显示了 SGM 成本函数和优化算法的具体实现方式。使用此伪代码段，可轻松评估内存、计算以及

图 12 来自 Middlebury 数据集的圆锥和面孔。使用简单的 SAD 法进行视差计算。视差在弯曲的表面上保持轻微变化，而在物体边界上剧烈变化。请查看右上角围栏的视差孔洞以及左边界其他物体的不连续性和遮挡情况

最终的硬件复杂性要求，从而支持基于 SGM 的实时计算。

图 13 用于实现 SGM 的伪代码