ZHCT356 September 2021 ADS8860 , OPA2991
1 简介
运算放大器电路通常在执行系统功能时需要响应输入和输出瞬态。部分电路主要设计用于接受不同的输入瞬态，如传感器信号调节电路；而其他电路则提供输出瞬态，例如模数转换器 (ADC) 输入或基准驱动器。在运算放大器电路设计中，同一电路的输出（负载）阶跃与输入阶跃的输出稳定响应时间的差异经常被忽视。
在大多数电路中，输出负载直接连接到运算放大器的输出端；响应时间在很大程度上基于运算放大器对所需负载瞬态及后续恢复提供支持的能力。然而，该行为取决于电路拓扑。在运算放大器输出电压 (Vopa) 不直接连接到负载的电路中，输出稳定响应会与输入响应大不相同。在放大器必须驱动容性负载 (Cload) 的情况下，此类电路的一个常见示例是具有双反馈 (Riso+DFB) 电路拓扑的隔离电阻器。在 Vopa 和 Cload 网络之间使用隔离电阻器 (Riso) 并存在从反馈电容器 (Cf) 和反馈电阻器 (Rf) 返回反相输入 (IN-) 的两个反馈路径，此电路也因此得名。
图 1-1 显示了一个用于驱动容性负载 (Cload) 的 Riso+DFB 电路示例。输入端直接连接到电压源，因此运算放大器必须对输入端发生的变化做出反应。在含有一个简单的开关 (SW1) 和电阻负载 (Rload) 的基本情况下，放大器电路必须对输出端出现的负载瞬态做出响应。
图 1-1 具有双反馈的 Riso 原理图图 1-2 中的两个仿真电路展示了输入阶跃和负载瞬态输出响应之间的差异。图 1-2(a) 将输入电压阶跃应用于电路的输入端，而 图 1-2(b) 将负载电流阶跃应用于输出端。在负载瞬态电路中，通过将流经 Riso (Iload x Riso) 的负载电流 (Iload) 形成的输出压降设置为与输入阶跃幅度相等，将两个电路中 Vopa 的初始变化设置为 10mV，从而实现同级比较。10mV 的输出阶跃幅度可防止运算放大器出现大信号趋稳行为，例如压摆率限制。此外，输出电流必须足够小，以防止运算放大器进入大信号短路电流限制范围。
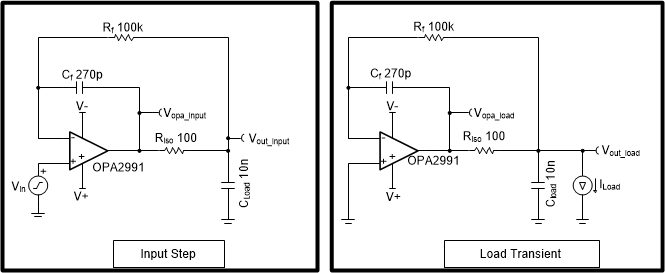图 1-2 输入阶跃 (a) 和负载瞬态 (b) 仿真电路图 1-3 显示了两个仿真电路的结果。按照设计，针对输入和输出响应，Vopa 的初始变化均为 10mV。但是负载输出电压 (Vout) 稳定所需的时间在两个电路之间是不同的；输入阶跃电路的趋稳速度比输出负载瞬态阶跃电路快得多。例如，若要稳定到 0.05%（相当于 10 位），输入阶跃电路需要 5.02µs，输出负载瞬态电路需要 189.42µs。
表 1-1 列出了图 1-2 中输入阶跃电路和负载瞬态阶跃电路要实现 10 至 18 位分辨率采集系统所需的输出稳定时间之间的差异。由于不同的输出阻抗和开环增益曲线会造成更加细微的影响，测试备选运算放大器将获得不同的稳定响应。
| 稳定精度级别 | 输入阶跃瞬态的稳定时间 (µs) | 负载瞬态的稳定时间 (µs) |
|---|---|---|
| 10 位 (0.05%) | 5.02 | 189.42 |
| 12 位 (0.01%) | 39.94 | 230.23 |
| 14 位 (0.003%) | 71.01 | 261.06 |
| 16 位 (0.00076%) | 106.45 | 289.23 |
| 18 位 (0.00019%) | 142.23 | 347.08 |
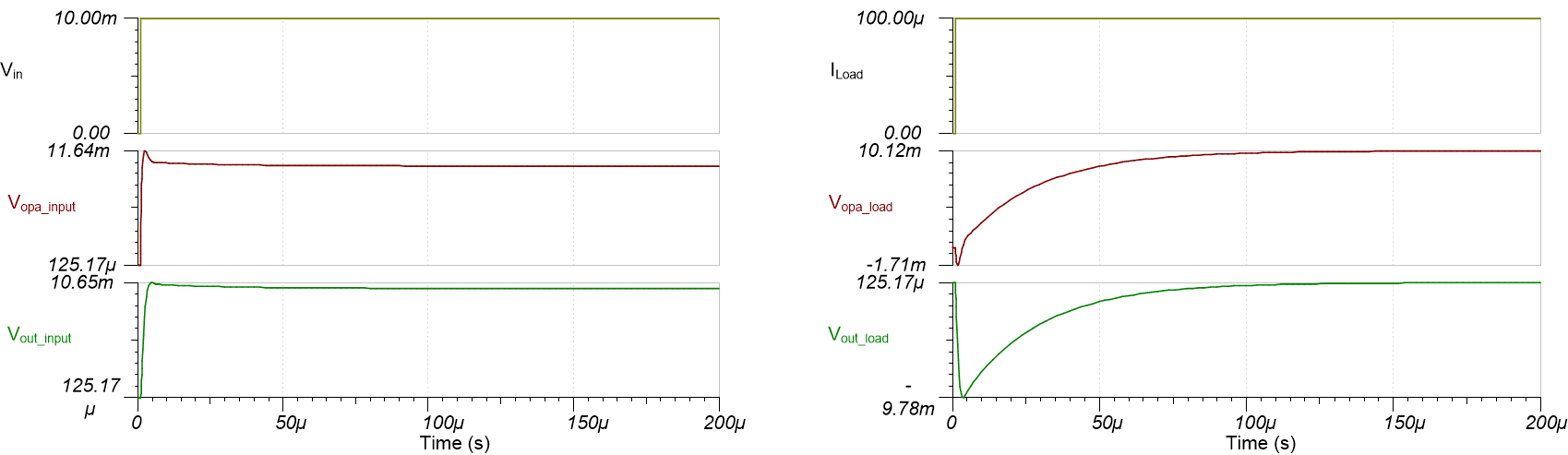图 1-3 输入阶跃 (a) 和输出负载瞬态 (b) 电路的输出稳定响应图 1-4 显示了对输入和输出瞬态的输出稳定响应起主导作用的元件，如红色箭头所示。对于输入阶跃瞬态，Riso 和 Cload 电阻-电容 (RC) 时间常数决定了输出稳定时间。发生输入阶跃时，Vopa 立即响应输入电压阶跃。随着运算放大器输出电压升高，Vout 会因 Riso 和 Cload 而出现延迟。
对于负载瞬态，Rf 和 Cf RC 时间常数决定了输出稳定响应。发生负载瞬态时，Vout 立即下降 10mV (Riso x Iload)。Vopa 响应 Vout 下降所需的时间取决于 Rf 和 Cf 产生的 RC 延时时间。
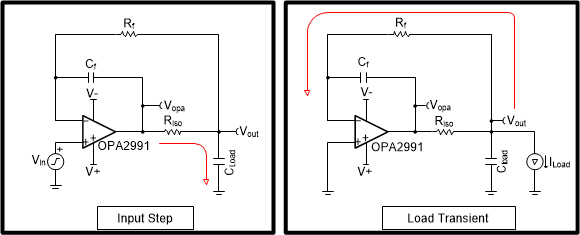图 1-4 主导输入阶跃 (a) 和输出负载 (b) 瞬态响应的 RC 时间常数图 1-5 将输入阶跃和负载瞬态输出稳定时间（底部响应）与前文所述的起主导作用的 RC 时间常数（顶部响应）进行了比较。图 1-5F(a) 将 Vout 的输入阶跃稳定时间与具有 100Ω 电阻器和 10nF 电容器（Riso 和 Cload）的 RC 电路响应进行了比较。图 1-5(b) 将输出瞬态稳定时间与具有 100kΩ 电阻器和 270pF 电容器（Rf 和 Cf）的 RC 电路响应进行了比较。RC 电路上升时间与输入阶跃和负载瞬态输出稳定响应一致，从而证实了上述理论。
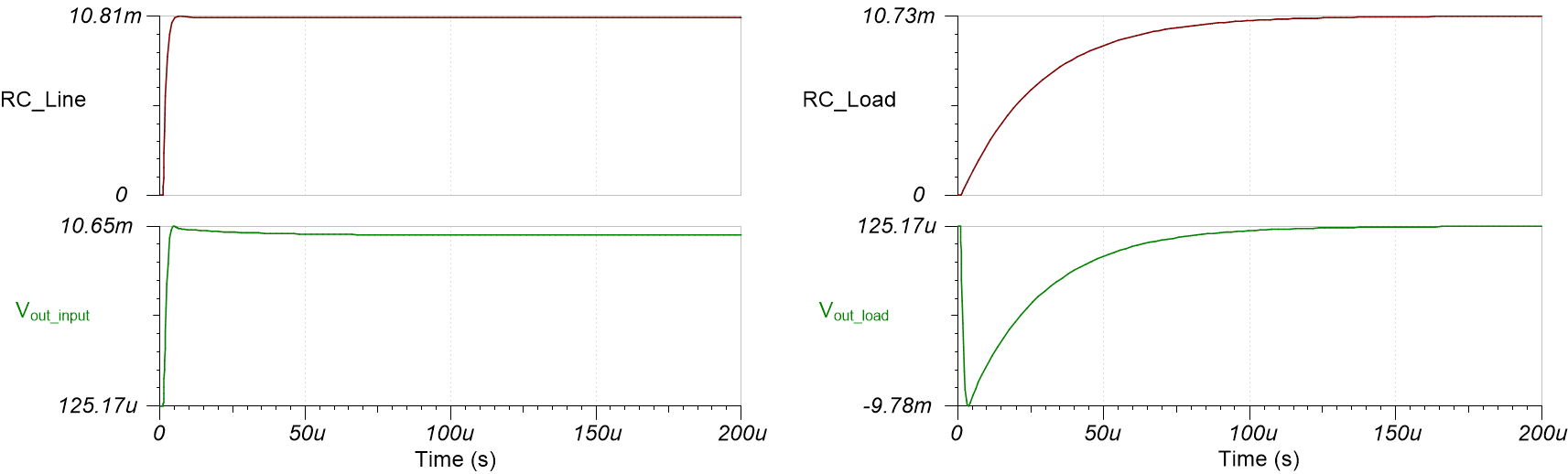图 1-5 输入阶跃 (a) 和输出负载 (b) 瞬态稳定时间（RC 时间常数起主导作用）下文将讨论 Riso+DFB 电路的稳定性标准，并介绍如何优化反馈比，以获得更好的负载瞬态稳定时间。首先，运算放大器作为单位增益缓冲器，必须稳定驱动 Riso+Cload 组合。其次，由 Rf 和 Cf 形成的 1/Beta 极点必须至少小于来自 Riso 和 Cload 的零点频率的一半。
- 单位增益缓冲器驱动 Riso x Cload 的相位裕度：>45°
- 反馈比：(Rf x Cf)/(Riso x Cload) > 2
有关稳定性理论的更多解释，请参阅 TI 高精度实验室视频：运算放大器稳定性。
虽然稳定运行的反馈路径的最小比率为 2，但稳定电路没有最大比率。只要满足第一个标准，反馈路径比率可稳定保持在 10、100 甚至 1,000，并具有类似的相位裕度结果。然而，如 图 1-5 所示，输出负载响应基于由 Rf 和 Cf 元件形成的时间常数。因此，虽然稳定，但较大的比率将导致负载响应比输入响应慢得多。
图 1-6 显示了输出稳定响应如何随改变 (Rf x Cf)/(Riso x Cload) 的比率而化变。当反馈比接近最小标准 2 时，输入阶跃和输出负载瞬态的输出响应几乎相等，但会增加一些过冲和振铃。增加 (Rf x Cf )/(Riso x Cload) 的比率会产生更大的阻尼输出，一旦比率大于 20，该输出对输入阶跃响应的影响最小。然而，该比率对 Rf x Cf 时间常数起主导作用，因此较大的比率会继续增加负载瞬态输出响应时间。
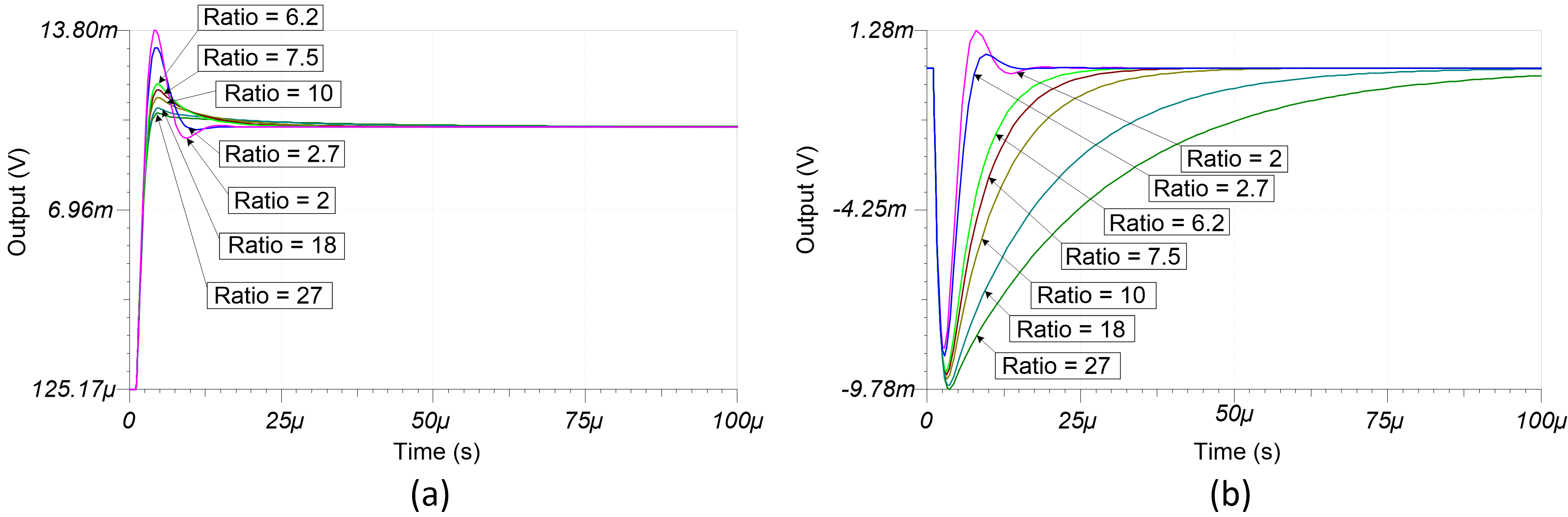图 1-6 输入阶跃（顶部）和输出负载（底部）瞬态的多个比率的输出稳定响应因此，为了在响应输出负载瞬态时实现卓越性能，应在设计电路时采用接近 2 的 (Rf x Cf )/(Riso x Cload) 比率。由于运算放大器特性与电路元件和多样性之间的相互作用将导致某些组合低于目标比率，更保守的设计方法将此比率设置在 4 和 10 之间。反馈元件比率低于 2 将影响电路的稳定性。
这种效应发挥作用的一个实际例子是 ADC 基准驱动电路，如图 1-7 所示。
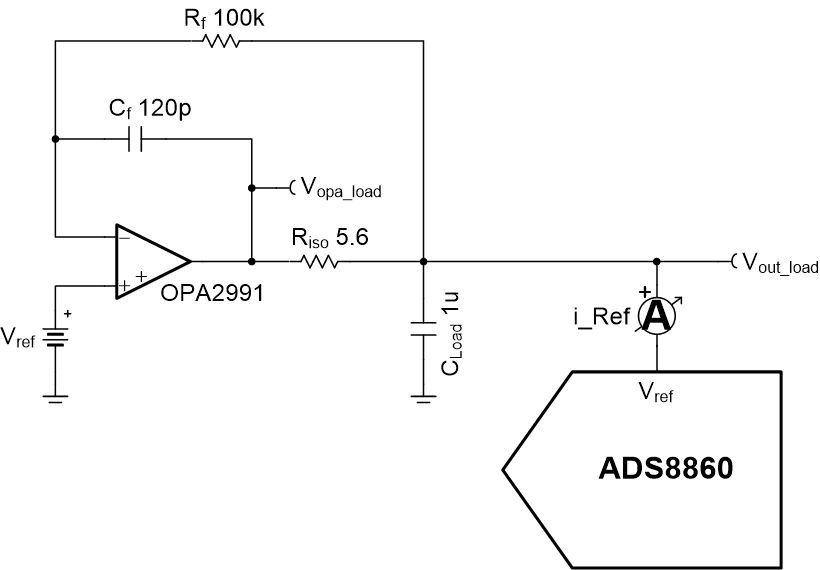图 1-7 ADC 基准驱动电路在 ADC 的转换阶段，逐次逼近过程中会将内部电容器数模转换器 (CDAC) 组切换到电路中。每次新的电容器切换到电路中时，外部驱动电路所需的电流突发将作为负载瞬态出现。因此，如果没有正确配置电路反馈比，Riso+DFB 电路可能无法正确稳定至负载响应。
图 1-8 显示了电路仿真中的上述效应，其中使用 图 1-7 中的运算放大器电路作为 ADS8860 的基准缓冲器，ADS8860 是一个 16 位逐次逼近寄存器 ADC，在本示例中配置为以 100kSPS 的速率进行采样。将电路中的反馈路径比值从大约 3.6 变化到 360 显示了负载稳定时间的差异。正如图 1-5 中的结果所预期，具有较高比率的电路需要更长的时间使基准缓冲器电路达到平衡，从而导致转换之间的最低有效位稳定误差小于 1/2。
最低模拟比率 – 图 1-8(a) 中的 3.6 – 需要大约四个样本达到平衡，而图 1-8(c) 中比率为 360，需要超过 400 个样本（或大约 4ms）电路才能达到平衡，这很好地说明这一点。应用通常采用间歇性的样本突发，对于具有图 1-8(c) 所示结果的电路可能不会在样本突发完成之前完全达到平衡。不稳定的基准会导致出现转换错误和 AC 性能下降。如前所述，比率为 3.6 和 360 的电路的相位裕度和输入响应几乎相同；如果您没有正确设计电路并验证输出负载响应，则可能会出现意外的电路结果。
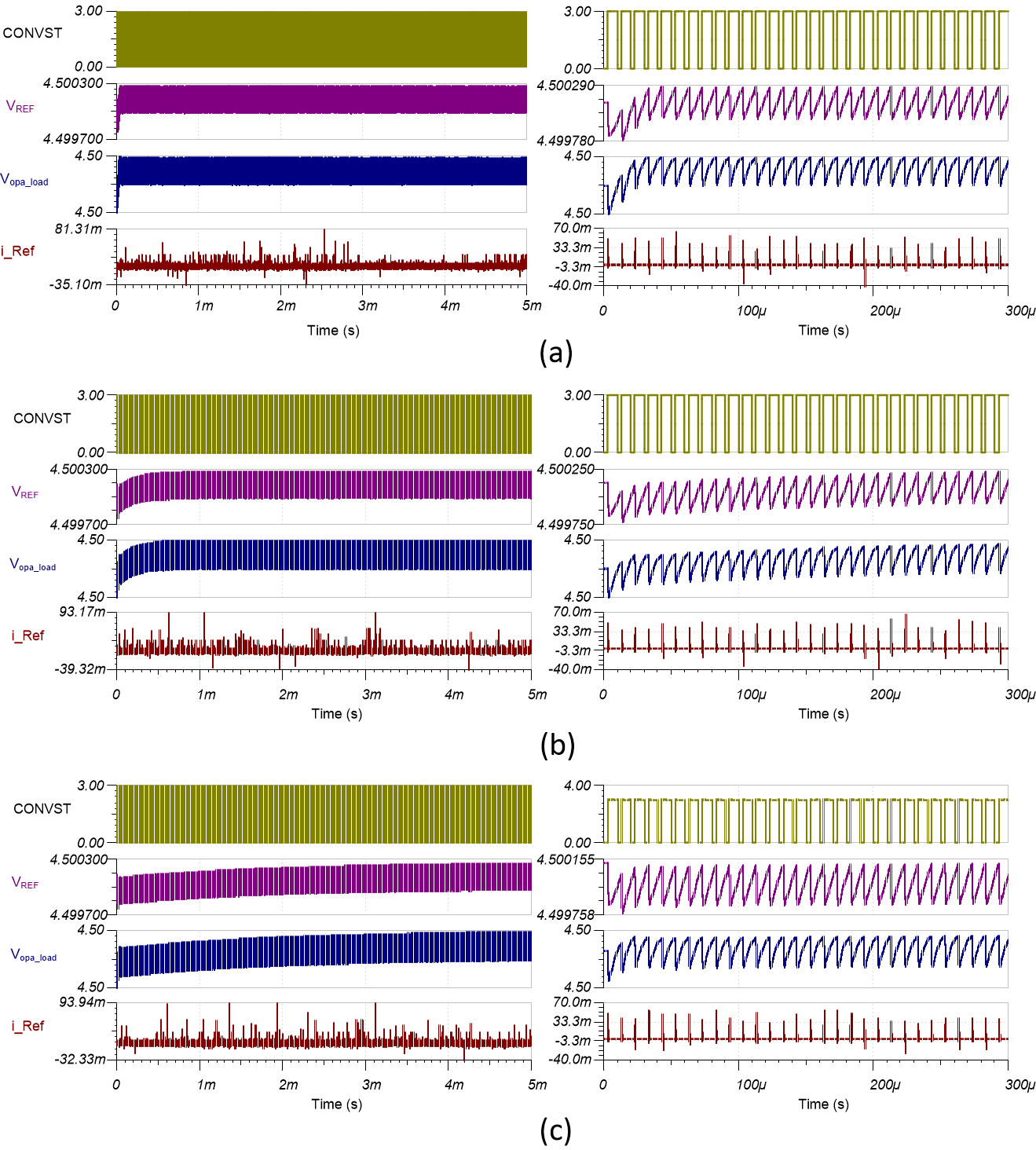图 1-8 不同反馈比率的 ADC 基准驱动趋稳：3.6 (a)；36 (b)；和 360 (c)。左图和右图分别显示了 5ms 时间标度和 300µs 时间标度，结果相同。