The most important elements to the closed-loop performance are the open-loop gain and open-loop output impedance. Figure 9-1 and Figure 9-2 show the simulated differential open-loop gain and phase from the differential inputs to the differential outputs with no load and with a 100-Ω load. Operating with no load removes any effect introduced by the open-loop output impedance to a finite load. This A_OL simulation removes the 0.6-pF internal feedback capacitors to isolate the forward path gain and phase (see Figure 13-1). The 0.6-pF capacitance becomes part of the feedback network that sets the noise gain and phase combined with the external elements. The simulated differential open-loop output impedance is shown in Figure 9-3.

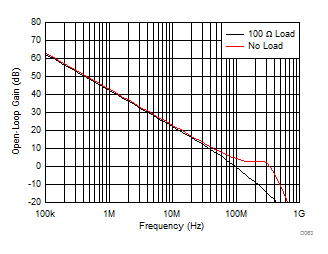Figure 9-1 No-Load and 100-Ω Loaded A_OL Gain

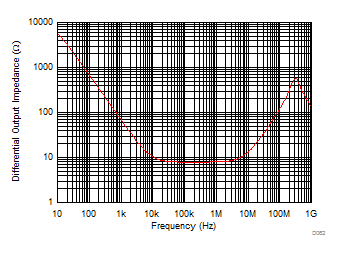Figure 9-3 Differential Open-Loop Output Impedance

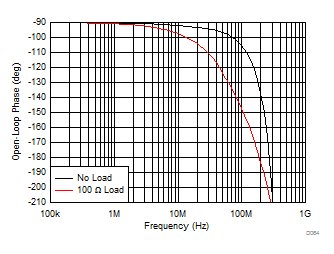Figure 9-2 No-Load and 100-Ω A_OL Phase

This impedance combines with the load to shift the apparent open-loop gain and phase to the output pins when the load changes. The rail-to-rail output stage shows a very high impedance at low frequencies that reduces with frequency to a lower midrange value and then peaks again at higher frequencies. The maximum value at low frequencies is set by the common-mode sensing resistors to be a 10.5-kΩ dc value (see Section 9.2). This high impedance at a low frequency is significantly reduced in closed-loop operation by the loop gain, as shown in the closed-loop output impedance of Figure 7-38. Figure 9-1 compares the no load A_OL gain to the A_OL gain driving a 100-Ω load that shows the effect of the output impedance. The heavier loads pull the A_OL gain down faster to lower crossovers with more phase shift at the lower frequencies.

The much faster phase rolloff for the 100-Ω differential load explains the greater peaked response illustrated in Figure 7-4 and Figure 7-22 when the load decreases. This same effect happens for the RC loads common with converter interface designs. Use the TINA-TI™ model to verify loop phase margin in any design.