KOKA004B january 2018 – july 2021 LF347 , LF353 , LM348 , MC1458 , TL022 , TL061 , TL062 , TL071 , TL072 , UA741
1.2 이상적인 연산 증폭기 모델
그림 1-1는 그림 1-2의 테브닌 증폭기 모델을 표준적 연산 증폭기 표기로 다시 그린 것입니다. 연산 증폭기는 차동 대 싱글 엔디드 증폭기입니다. 입력 포트 상에서 전압 차이 Vd = Vp - Vn을 증폭해서 출력 포트 상에서 전압 Vo를 발생시키고 접지로 참조합니다.
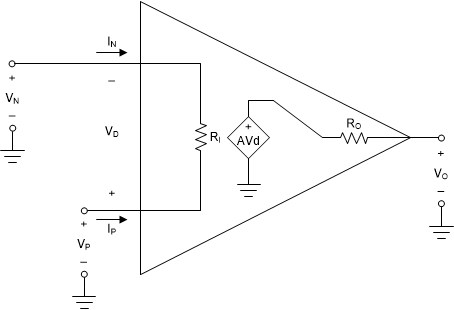 그림 1-2 표준적 연산 증폭기 표기
그림 1-2 표준적 연산 증폭기 표기위에서도 언급했듯이 입력 포트와 출력 포트로 부하 효과가 존재합니다. 이상적 연산 증폭기 모델을 사용해서 회로 계산을 단순화할 수 있으며, 이 방법이 엔지니어들이 일차적으로 대략적인 계산을 하기 위해서 흔히 사용하는 방법입니다. 이상적 모델은 단순화를 위해서 다음과 같은 세 가지 가정을 합니다:
- 이득이 무한대이다방정식 1. a = ∞
- 입력 저항이 무한대이다방정식 2. Ri = ∞
- 출력 저항이 0이다방정식 3. Ro = 0
그림 1-2로 이러한 가정들을 적용하면 그림 1-3과 같은 이상적인 연산 증폭기 모델을 얻을 수 있습니다.
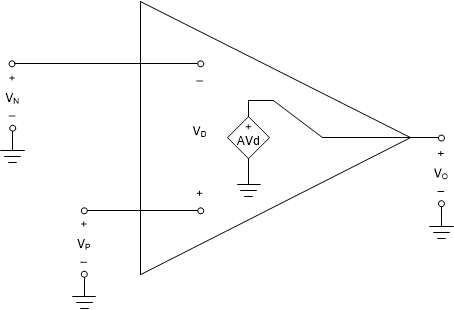 그림 1-3 이상적 연산 증폭기 모델
그림 1-3 이상적 연산 증폭기 모델이러한 이상적 연산 증폭기 모델을 사용해서 또 다른 단순화들을 할 수 있습니다:
Ri = ∞이므로 In = Ip = 0이라고 가정합니다. 그러므로 입력에서 부하 효과가 없습니다.
Ro = 0이므로 출력으로 부하 효과가 없습니다.
연산 증폭기가 선형적 동작을 한다면 V0은 유한한 전압일 것입니다. 정의에 따라 Vo = Vd × a. 재배열하면, Vd = Vo / a. a = ∞, Vd = Vo / ∞ = 0이므로 이것이 가상 단락 개념의 토대입니다.
이상적 전압 소스를 사용해서 출력 포트를 구동하면 입력 포트 상의 전압 차이만 작용할 것입니다. Vn과 Vp로 공통적 전압은 제거됩니다.
주파수 종속성은 없는 것으로 간주합니다.
시간, 온도, 습도, 전원 변동 등에 대해서 성능 변화가 없는 것으로 간주합니다.