방정식 24로 방정식 1의 a = ∞를 대입하면 다음과 같습니다.

방정식 27.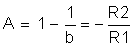

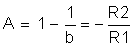
방정식 6에서 V_n과 V_p 사이의 전압 차이 V_d가 0인 것으로 가정했던 것을 상기하면, V_n = V_p입니다. 그렇지만 단락된 것은 아닙니다. 이것을 V_n과 V_p 사이에 가상 단락이라고 합니다. 가상 단락 개념을 사용해서 그림 3-1의 반전 연산 증폭기 회로 분석을 더더욱 단순화할 수 있습니다.

가상 단락 개념을 사용하면 다음과 같다고 할 수 있습니다.

이 구성으로는 반전 입력이 가상 접지입니다.

반전 입력에서 노드 공식은 다음과 같습니다.

방정식 29.

V_n = 0이므로 공식을 재배열해서 다음과 같이 A를 구할 수 있습니다.

방정식 30.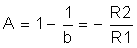

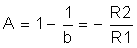
동일한 결과를 방정식 24에서보다 더 손쉽게 도출할 수 있습니다. 가상 단락(또는 가상 접지) 개념을 사용해서 그림 3-1에서 보는 반전 증폭기 계산을 단일 노드 공식을 푸는 것으로 단순화할 수 있습니다.