2 Δ-Σ ADC 中的数字滤波器

要了解数字滤波器为何在 Δ-Σ 模数转换中具有重要作用，就需要对 Δ-Σ 调制器有基本的了解。调制器从采样保持电路获取输入，该电路将以比 ADC 输出数据速率 (f_DR) 快很多倍的速率 (f_MOD) 对 ADC 输入进行采样。

调制器包含至少一个积分器和一个低分辨率 ADC，后者将积分器输出电压量化为仅几位。调制器将低分辨率 ADC 的输出转换回模拟量，并将其反馈回调制器输入，然后减去输入电压，作为误差校正的一种方式。结果是一个离散时间反馈系统，此系统允许采样输入信号以单位增益传递，但会使量化噪声密度在低频时更低，在高频时更高。

为了降低更高频率的量化噪声，调制器输出会馈送到数字低通滤波器。随后，目标信号会传递到数字滤波器的输出，同时滤除大部分更高频率的量化噪声。

图 2-1 展示了使用 Δ-Σ ADC 中一种常见低通数字滤波器（称为 sinc 滤波器，其名称源于其 sin(x) / x 频率响应）的响应而绘制出的量化噪声。

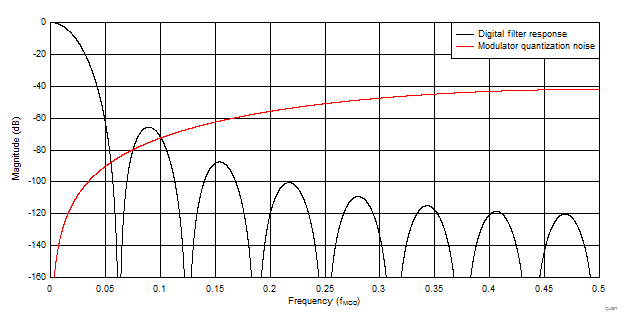图 2-1 Δ-Σ 量化噪声的频谱和 sinc 低通滤波器

Sinc 滤波器虽然极其常见，但它并不是唯一用于 Δ-Σ ADC 的数字低通滤波器类型。例如，一些 ADC（如 ADS124S08）添加了一个额外的 50Hz 和 60Hz 陷波滤波器，旨在用于具有大量电力线干扰的应用。另一方面，ADS127L01 具有一个宽带宽平坦通带数字滤波器，旨在用于频率更高的应用。

Δ-Σ ADC 中的数字滤波器具有另一个功能 – 抽取。这些滤波器按照一个称为过采样率 (OSR) 的因数以 f_MOD 的频率抽取从调制器输出的数据。f_DR 和 f_MOD 之间的关系是 f_DR = f_MOD / OSR。OSR 和滤波器类型共同决定了数字滤波器的输出带宽和 ADC 的整体频率响应。大 OSR 产生小滤波器带宽，意味着可获得非常好的噪声性能、简化的抗混叠电路以及更低的主机控制器数字接口速度。

Δ-Σ ADC 中的大多数数字滤波器具有有限脉冲响应 (FIR)。这些滤波器本质上很稳定且易于设计，具有线性相位响应。图 2-2 和图 2-3 并排绘制了 Δ-Σ ADC 中两种类型 FIR 滤波器的响应。图 2-2 对应 ADS127L01 中的宽带滤波器。图 2-3 是一款经典的三阶 sinc 响应滤波器或 sinc³，与 ADS124S08 中的滤波器类似。

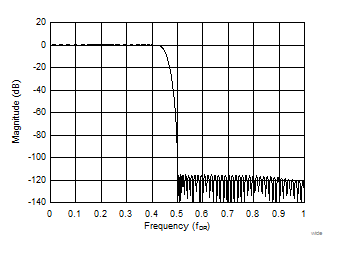图 2-2 宽带滤波器频率响应

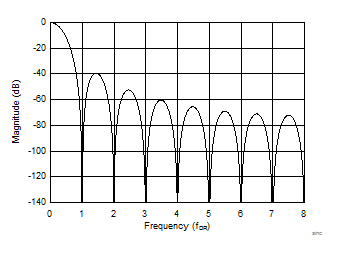图 2-3 Sinc³ 频率响应

在交流测量应用中使用宽带滤波器的好处可以从其幅度响应中明显看出。它的增益在接近数据速率的奈奎斯特带宽 (f_DR /2) 之前一直是接近 0dB，这样可确保信号频率在通带内不会有信号功率损耗。陡峭过渡频带限制了混叠。另一方面，sinc³ 滤波器在 0.262 x f_DR 时使信号衰减至 –3dB，即使在 f_DR/2 之后也会缓慢过渡，这将使更多的带外噪声混叠到目标带宽中。从表面上看，宽带 FIR 滤波器是各种应用的理想选择；然而，这种出色的频域性能是有代价的。

应在时域方面对宽带滤波器和 sinc 滤波器进行权衡。宽带滤波器是一种非常高阶的滤波器，这意味着在接收一个阶跃输入后需要很长时间才能稳定至最终值。在 ADS127L01 的宽带滤波器中，需要进行 84 次转换才能实现稳定的输出。sinc³ 滤波器在输入端阶跃后进行三次转换即可稳定，从而可在多个输入通道之间快速进行周期运行。所有 FIR 滤波器需要在频率响应和延迟之间进行权衡。