ZHCACL7A january 2021 – april 2023 TMAG5170 , TMAG5170-Q1 , TMAG5170D-Q1 , TMAG5173-Q1 , TMAG5273
2.3 CORDIC 角度估算
CORDIC(即坐标旋转数字计算器)为数字系统使用坐标数据计算角度提供了一种快速有效的方法。该算法通过执行二进制搜索以围绕原点旋转一个点,直到生成的矢量位于单个轴上,从而快速近似计算角度。由于坐标输入以迭代阶跃旋转,因此可以通过所有阶跃的总和来估算起始角度。完成这些旋转后产生的结束位置也将产生输入矢量的大小。当与多轴霍尔效应传感器的输出一起使用时,该算法被证明是快速且精确的角度计算的极佳选择。考虑图 2-8 中的点。
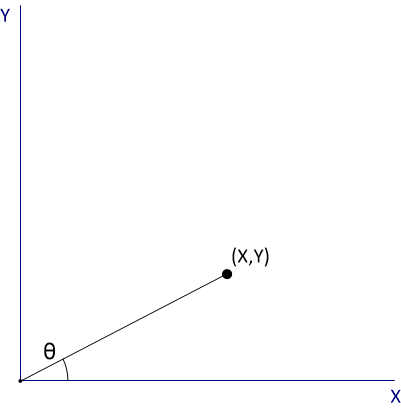 图 2-8 CORDIC 输入
图 2-8 CORDIC 输入如果将该点顺时针旋转 45°(表示为 α0),则新生成的矢量将离开第一象限,如图 2-9 所示。
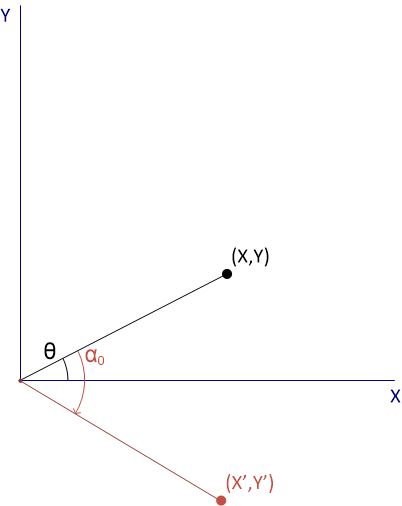 图 2-9 CORDIC 第一个阶跃
图 2-9 CORDIC 第一个阶跃由于目标是将矢量与 X 轴对齐,因此在下一个阶跃中必须逆时针调整旋转方向。在下一次迭代中,坐标将逆时针旋转 22.5° (α1)。此处的结果不会产生象限变化,因此旋转方向会继续沿此方向。此过程继续进行,添加和减去角度阶跃并更改旋转方向,直到结果与 X 轴对齐。如图 2-10 所示,5 次迭代后的近似角度约为 19.69°。
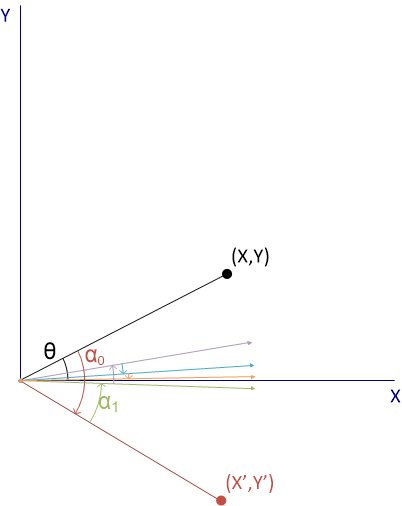 图 2-10 CORDIC - 5 次迭代
图 2-10 CORDIC - 5 次迭代在方程式 1 中的矩阵乘法之后描述了在空间中旋转坐标点的代数过程。
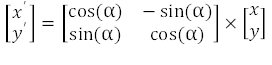
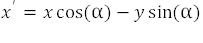
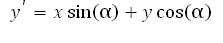
如果从结果乘积中分解出 cos(α) 因子,那么我们将得到公式 4 和 5:
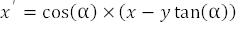
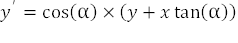
随着算法的进行,我们必须确定旋转的方向。如果我们选择逆时针旋转,结果将产生公式 6 和 7:
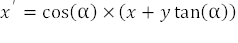
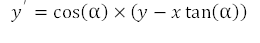
请注意,此处唯一的区别是每个公式中的运算是反转的。因此,我们可以通过检查操作符号轻松确定旋转方向。该旋转可以由一个可选值表示,我们将其表示为 d。
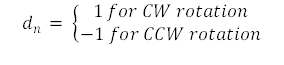
此时,一些近似值可简化角度计算。如果 cos(α) 被完全移除,检查结果将显示已创建一个新矢量,该矢量旋转了正确的角度但大小大于原始矢量。该因子实际上是一个标量,用于将生成的矢量归一化为循环的每个阶跃的正确大小。标量值由旋转角度决定,可使用预先确定的阶跃大小针对每个阶跃轻松计算。
如果对每个角度转换使用固定次数的迭代,则每个矢量转换的累积乘积将始终产生恒定的最终标量 m。因此,在例程中可以忽略 cos(α) 的值。相反,最终的大小结果可以按 m 缩放一次。假设使用算法的十次迭代(0 至 9),则 m 的结果值如公式方程式 9 所示。
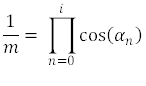
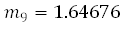
此外,我们可以注意到 tan(α) 接近于 2-n 的值。如果将正切计算替换为乘以 2 的幂,则该算法的实现将变得更加简单。考虑以下值表:
|
αn [°] |
tan(α) |
2-n |
tan-1(2-n) [°] |
|---|---|---|---|
|
45 |
1 |
1 |
45 |
|
22.5 |
0.414 |
0.5 |
26.565 |
|
11.25 |
0.199 |
0.25 |
14.036 |
|
5.625 |
0.098 |
0.125 |
7.125 |
|
2.8125 |
0.049 |
0.0625 |
3.576 |
对算法进行这些修改后,我们得到方程式 11 至方程式 14,可以迭代使用这些公式来确定任何二维矢量的角度和大小。
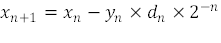
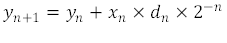
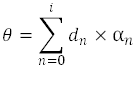

请注意,该方法仅使用了少数几次循环,为快速计算提供了一种简洁的解决方案。集成了 CORDIC 引擎的器件(例如 TMAG5170)能够快速解析角度计算并将其作为输出提供,而不会对整体转换时序产生任何重大影响。