系统设计人员希望使用多路复用器来实现简单的信号路由，并且希望物理多路复用器对信号本身的影响尽可能小。输入信号与输出信号形状之间与时间相关的差异通常称为失真。如果输入信号的部分频率分量超过系统带宽，系统对这部分信号的响应会滞后。因此，输出信号无法准确再现输入信号中最快的变化。这导致输出信号的幅度可能降低，边沿比输入信号中的相应特征更宽、更圆。

本节将研究方波，以了解方形波的形成原因。复杂的波形可以由不同振幅和相位关系的正弦波（以及余弦波）组合而成。这就是傅里叶分析的基础。

例如，方波可以由多个不同频率的正弦波组合而成。除了基频外，这些添加的正弦波称为谐波；方波的谐波是基频的奇数倍。随着更多高次谐波的加入，波形会越来越接近理想的方波。

谐波的振幅等于 1/N，其中 N 为谐波的级数（1、3、5、7…）。每个谐波与基波具有相同的相位关系。如果只使用前两个谐波来构造方波，则可以初步看到方波的形成过程（图 2-2 中的波形 B）。在图 2-2 中，红色轨迹表示理想的方波波形，绿色轨迹表示包含正确振幅的 N 次谐波的波形。干扰频率必须远高于基频。如果系统需要通过第三、第五甚至更高次的谐波，3dB 截止频率必须高于这些谐波，即基频的三倍、五倍或七倍以上。  如果使用第五次谐波（零、三和五）来构造方波，方波开始逐渐成型（图 2-2 中的波形 C）。如果使用超过第十次谐波来构造方波，波形将非常接近理想的方波（图 2-2 中的波形 D）。

从这些图中可以很容易看出，方波的形状是由高频谐波成分而不是直流分量决定的。

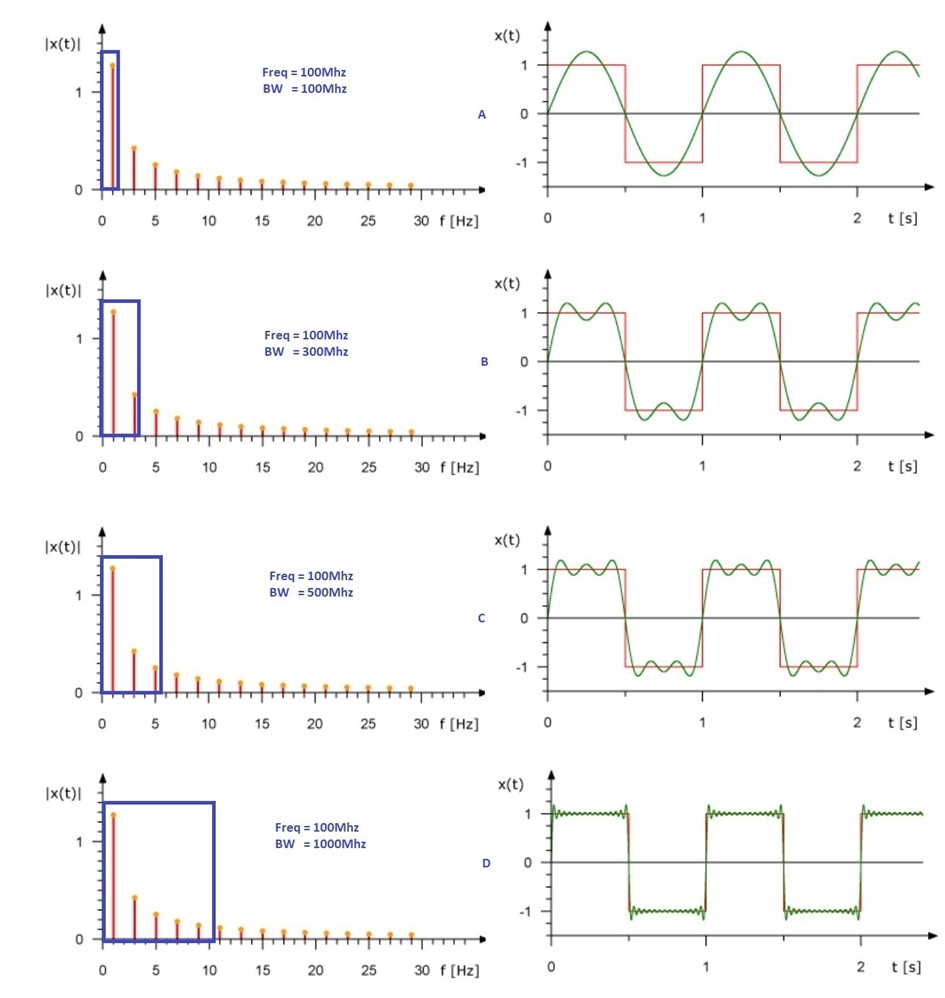图 2-2 由不同谐波构成的方波